Введение
При выборе направления исследовательской работы я руководствовался тем, что мне интересны точные науки. Я посчитал важным при подготовке результатов работы повышение своего уровня пользования математических программ и навыка алгоритмизации (программирования). При чтении литературных источников я нашел область математики, которая изучается в 9-м классе, и рассматривает пласт задач, направленных на перебор возможных вариантов решений.
Согласно Бродскому [1], область математики, в которой изучается вопрос о том, сколько различных конфигураций, удовлетворяющих тем или иным условиями, можно составить из заданных объектов, называют комбинаторикой.
Математический аппарат комбинаторики успешно применяется в теории вероятностей, математической статистике, экономике, лингвистике, программировании, биологии и других науках. Например, нижеупомянутые биноминальные коэффициенты применялись ученым Г. Гамовым в теории белкового кода, которая способствовала разгадке генетического кода (Виленкин, 1969).
Многие авторы выделяют три типичных вида комбинаторных задач. Например, (Халамайзер, 1980) описал их как:
— составление перестановок (образование упорядоченных множеств), состоящее в установлении определенного порядка следования элементов множества друг за другом;
— составление сочетаний (образование подмножеств), состоящее в выделении из данного множества некоторой части его элементов (термин сочетания был введен Б. Паскалем в XVII веке (Бродский, 2008));
— составление размещений (образование упорядоченных подмножеств).
В основе решений вышеперечисленных задач лежит математический аппарат, включающий в себя действия с функциями n!, A n , C n . Числа A n и C n связаны между собой, но в то же время число C n имеет больший практический интерес. Поэтому объектом исследования я выбрал именно это число, которое также называют биноминальным коэффициентом.
Цель работы: изучение индивидуальных свойств биноминальных коэффициентов.
Гипотеза : предположим, что изучение свойств биноминальных коэффициентов упрощает решение комбинаторных задач и теории вероятностей
Задачи:
— Теоретическая подготовка вопроса о методах расчета биноминальных коэффициентов.
— Расчет биноминальных коэффициентов для разложения бинома Ньютона первых 50-ти степеней.
— Определение круга функций MS Excel необходимых для проведения вычислений.
— Нахождение характеристик биноминальных коэффициентов, а именно распределений зависимостей
— Теоретический анализ темы
— Практический расчет в электронных таблицах
Методы исследования : измерение, сравнение
Объект исследования: биноминальные коэффициенты
Предмет исследования: индивидуальные свойства биноминальных коэффициентов.
Актуальность: индивидуальные свойства биноминальных коэффициентов актуальны для работы в комбинаторике, теории вероятностей, математической статистике и алгебре. Они помогают упростить вычисления, анализировать результаты экспериментов и выражения, а также предсказывать будущие события.
1 Биноминальные коэффициенты
1.1 Формула Ньютона
Впервые знакомство с биноминальными коэффициентами происходит в 7 классе, когда изучали тему «Формулы сокращенного умножения». Действительно, в формуле (a+b)²=a²+2ab+b², постоянные коэффициенты в правой части являются числами

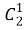
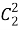
Формула разложения бинома с действительным показателем степени была выведена в 1678 году Исааком Ньютоном. Отметим, что для целых чисел формула была известна в середине XVI века (Халамайзер, 1980). В общем виде формула выглядит следующим образом:

В упрощённом для вычислений виде формулу можно записать следующим образом:
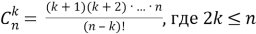
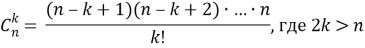
Математический смысл биноминального коэффициента — это количество подмножеств, содержащее k элементов, выбранных из множества, состоящего из n элементов (Макарычев, 2008). Еще подобные выборки называют неупорядоченными выборками или сочетаниями (Бродский, 2008).
Например, пусть дано множество из четырех элементов {A,B,C,D}, тогда возможные подмножества из трех элементов будут: {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}. Количество этих подмножеств соответствует числу
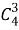
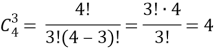
1.2 Треугольник Паскаля
Одним из графических представлений биноминальных коэффициентов является треугольник Паскаля (рисунок 1). У некоторых авторов этот треугольник встречается под другими именами: таблица Тартальи (Руэ, 2014), арифметический треугольник (Виленкин, 1976). Треугольник был известен в древних Китае, Индии, Персии примерно в XII-XIII веках.
Правило построения данного треугольника просты (Виленкин, 1976):
— Новый элемент вычисляется как сумма чисел предыдущей строки, стоящих слева и справа от этого элемента;
— Если элемента выше не существует, то его значение принимается за ноль.
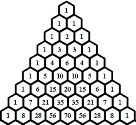
Рис. 1. Треугольник Паскаля
Математический смысл элемента треугольника Паскаля — это количество способов, которыми можно попасть из вершины треугольника в точку с этим элементом при условии движения только вниз (Руэ, 2014). Основные свойства треугольника Паскаля:
— Количество элементов каждой строки на 1 больше, чем номер строки (нумерация строк начинается с нуля)
— Элементы в строке располагаются симметрично;
— Каждый элемент треугольника Паскаля соответствует биноминальному коэффициенту, где n — номер строки, k — номер элемента строки.
1.3 Закономерности биноминальных коэффициентов
В XVII веке Ньютон показал следующие разложение в ряд двучлена (бинома), возведённого в степень:

Данная формула получила название бином Ньютона (Руэ, 2014).
Биноминальные коэффициенты имеют свойства, рассмотренные во многих источниках. Например, Виленкин, 1975, Виленкин, 1976, Халамайзер, 1980, Бродский, 2008. Кратко перечислим их:
- число членов разложения на единицу больше показателя n;
-
коэффициенты членов разложений, равноудаленных от концов, равны между собой, т. е.
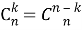
-
сумма всех биноминальных коэффициентов в строке равна 2n, т. е.
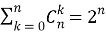
- сумма биноминальных коэффициентов, стоящих на четных местах, равна сумме биноминальных коэффициентов, стоящих на нечетных местах, причем каждая из этих сумм равна 2n-1;
-
если удовлетворяется условие 0 ≤ k ≤ n, то выполняется равенство
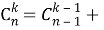

В тоже время в литературных источниках не было найдено разбора свойств самих биноминальных коэффициентов. Поэтому в ходе выполнения этой работы я надеялся провести анализ этих свойств.
1.4 Способы вычисления биноминальных коэффициентов
Для анализа биноминальных коэффициентов был произведен их расчет двумя различными методами, основанными на принципе построения треугольника Паскаля и на использовании формулы Ньютона для

В результате было построено две таблицы размерами 51х50 с заполнением части таблицы, лежащей ниже главной диагонали (незаполненная часть таблицы не имеет математического смысла).
Отметим, что вычисление коэффициентов через треугольник Паскаля не требует особых усилий и использует только операцию сложения. С другой стороны, вычисление этим способом рекурсивное, то есть вычисление коэффициентов определенной строки невозможно без знаний коэффициентов предыдущего разложения.
Вычисление любого коэффициента через формулу Ньютона возможно на основе знаний его порядкового номера, но математический аппарат сильно усложняется. Использование факториала на этапе вычисления приводит к операции с большими числами, что затрудняет расчет биноминального коэффициента без использования вычислительной техники.
Для расчета биноминальных коэффициентов через формулу Ньютона использовалась функции MS Excel представленные в таблице 1 (здесь и далее описания функций MS Excel даны в соответствии со справочной системой этого программного продукта).
Таблица 1
Список функций MS Excel
|
№ |
Название функции |
Описание |
|
1 |
ФАКТР |
Возвращает факториал числа. |
|
2 |
ЧИСЛКОМБ |
Используется для определения общего числа всех групп, которые можно составить из элементов данного множества. |
После вычисления было проведено сравнение коэффициентов двух таблиц между собой, в результате которого мы убедились в их идентичности.
Для удобства дальнейших вычислений было решено перевести рассчитанные коэффициенты в столбчатое представление, при котором данные располагались в трех столбцах:
— номер строки (n);
— порядковый номер коэффициента (k);
— значение коэффициента (
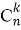
В отличии от табличного вида, столбчатый вид позволяет рассматривать любой коэффициент вне зависимости от его месторасположения.
2 Исследования зависимостей
2.1 Зависимость количества коэффициентов от номера строки
Согласно формуле разложения бинома Ньютона, итоговый многочлен должен иметь степень n. Учитывая, что многочлен содержит свободный коэффициент, получаем, что разложения бинома Ньютона n степени должно содержать n+1 биноминальных коэффициентов.
Хотя данный подсчет зависимости количества членов многочлена интуитивно понятен, и легко доказывается аналитическим путем, проведение этого эксперимента позволит выявить возможные ошибки расчета коэффициентов и начать ознакомление с MS Excel и его функциями.
Таблица 2
Список функций MS Excel
|
№ |
Название функции |
Описание |
|
1 |
СЧЁТЕСЛИ |
Подсчет значений диапазона, удовлетворяющих заданному критерию. |
С помощью функции, представленной в таблице 2, мы получили количество коэффициентов для разложения каждой степени. Как видно из рисунка 2, данная зависимость — линейная и пересекает ось ординат в значении 1.
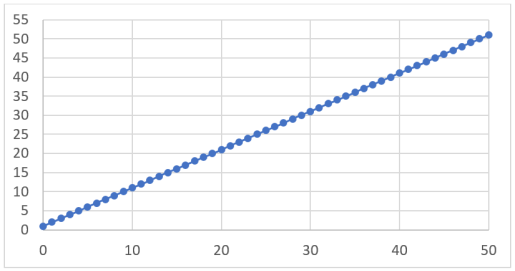
Рис. 2. График зависимости количества коэффициентов от степени бинома Ньютона
2.2 Зависимость суммы коэффициентов от номера строки
Данная зависимость упоминается различными авторами как одно из свойств биноминальных коэффициентов (Бродский, 2008, Халамайзер, 1980). В упомянутых источниках можно найти аналитическое доказательство равентсва:

Хотя данное равенство не нуждается в численной проверке, было решено ее провести для дальнейшего ознакомления с функциями MS Excel.
Таблица 3
Список функций MS Excel
|
№ |
Название функции |
Описание |
|
1 |
СУММЕСЛИ |
Подсчет суммы значений диапазона, удовлетворяющих заданному критерию. |
С помощью функции, представленной в таблице 3, мы получили сумму коэффициентов для разложения бинома Ньютона первых 50 степеней. Как видно из рисунка 3, данная зависимость — показательная. Так как показательная функция резко возрастает, на графике ненулевые значения начинаются с n=44.
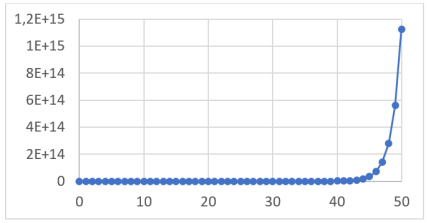
Рис. 3. График зависимости суммы коэффициентов от номера строки
Часто для удобства анализа графиков с показательной зависимостью используется логарифмический масштаб оси ординат. В нашем случае основание логарифмического масштаба равно двум.
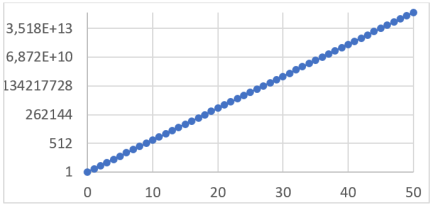
Рис. 4. График зависимости суммы коэффициентов от номера строки в логарифмическом масштабе
Как видно из рисунка 4 в логарифмическом масштабе зависимость — линейная, что подтверждает аналитический вывод о равенстве суммы биноминальных коэффициентов целочисленной степени числа 2.
2.3 Соотношение четных коэффициентов к нечетным
В этом пункте будет рассмотрено соотношение четных коэффициентов к нечетным. Исходным материалом будут служить рассчитанные коэффициенты до n=50 включительно, представленные в столбчатом виде.
Чётное число — целое число, которое делится на 2 без остатка. Для расчета чётного и нечётного коэффициентовиспользовалась функции MS Excel представленные в таблице 4. Принцип расчета четности числа основывался на нахождении остатка при делении числа на 2: если остаток был равен 0, то число считалось четным.
Таблица 4
Список функций MS Excel
|
№ |
Название функции |
Описание |
|
1 |
ОСТАТ |
Возвращает остаток от деления аргумента «число» на значение аргумента «делитель». |
|
2 |
СЧЁТЕСЛИ |
Подсчет значений диапазона, удовлетворяющих заданному критерию. |
В результате обработки массива было получено 1326 значений четных и нечетных коэффициентов. Для проведения анализа строки были объедены в пять групп. Полученные значения представлены в таблице 5.
Таблица 5
Соотношение четных коэффициентов к нечетным
|
Группа строк |
Четные коэффициенты |
Нечетные коэффициенты |
Четные коэффициенты, % |
Нечетные коэффициенты, % |
|
1–10 |
29 |
37 |
43,9 |
56,1 |
|
1–20 |
128 |
103 |
55,4 |
44,6 |
|
1–30 |
285 |
211 |
57,5 |
42,5 |
|
1–40 |
560 |
301 |
65,0 |
35,0 |
|
1–50 |
826 |
413 |
66,7 |
33,3 |
Мы можем увидеть, что в первой группе состоящей из первых десяти строк четные коэффициенты составляли примерно 44 % от общего количества коэффициентов. Уже в следующей группе с первой до двадцатой строки у нечетных коэффициентов небольшое отставание от четных. На этом этапе можно сделать предположение, что при дальнейшем увеличении степени бинома Ньютона доля четных коэффициентов будет только увеличиваться.
Как видно из таблицы 5, если во второй группе разность была 10,8 %, то в третьей группе 14,9 %, в четвертой 30,1 %. Всего во всех 50 строках количество четных коэффициентов была в 2 раза больше, чем нечетных. На рисунке 5 представлено изменение соотношения четных и нечетных коэффициентов.
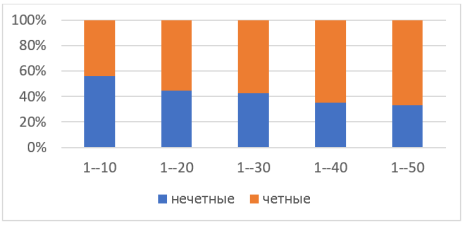
Рис. 5. График соотношения четных коэффициентов к нечетным
2.4 Распределение цифр коэффициентов
В этом пункте будет рассмотрено распределение цифр, из которых состоят биноминальные коэффициенты. Исходным материалом являются рассчитанные коэффициенты до n=50 включительно, представленные в столбчатом виде.
Алгоритм расчета состава чисел был основан на переводе числа в текст и анализа количества вхождений тех или иных цифр. В результате была получена таблица, где для каждого биноминального коэффициента было получено количество вхождений каждой цифры от 0 до 9. Для получения количества определенной цифры в числе, в символьном представлении числа эта цифра заменялась символом пустоты. Разница между длиной текстового представления числа до и после замены показывала количество вхождений цифры в это число. Общее число вхождений определенной цифры в написание биноминальных коэффициентов рассчитывалась как сумма столбца этой таблице.
Для расчета цифр составляющих числа биноминальных коэффициентов использовались функции MS Excel представленные в таблице 6.
Таблица 6
Список функций MS Excel
|
№ |
Название функции |
Описание |
|
1 |
ТЕКСТ |
Преобразует значение в текст в заданном числовом формате. Данная функция применялась с параметром 0, который определял формат исходного значения как целое число. |
|
2 |
ДЛСТР |
Возвращает число символов в текстовой строке. |
|
3 |
ПОДСТАВИТЬ |
Заменяет новым текстом старый текст в текстовой строке. |
|
4 |
СУММ |
Суммирует значения. |
В результате обработки 1326 биноминальных коэффициентов мы получили 9102 цифры, из которых они состоят. Частоту встречаемости каждой цифры можно увидеть в таблице 7 и на рисунке 6.
Таблица 7
Распределение цифр коэффициентов
|
Цифра |
Кол-во вхождений |
|
0 |
1221 |
|
1 |
1169 |
|
2 |
928 |
|
3 |
854 |
|
4 |
874 |
|
5 |
929 |
|
6 |
931 |
|
7 |
748 |
|
8 |
803 |
|
9 |
645 |
Из таблицы 7 видно, что тройка самых встречаемых цифр: 0 (13,41 % от общего числа цифр), 1 (12,84 %), 6 (10,23 %). Отметим, что цифры 5 и 2 встречаются практически также как и цифра 6 располагающиеся на третьем месте. Самые редкие цифры используемы при написании биноминальных коэффициентов это 8 (8,82 %), 7 (8,22 %), 9 (7,09 %). Любопытно, но самая редкая цифра 9 встречается в написании коэффициентов в первый раз самой последней (при n=9).
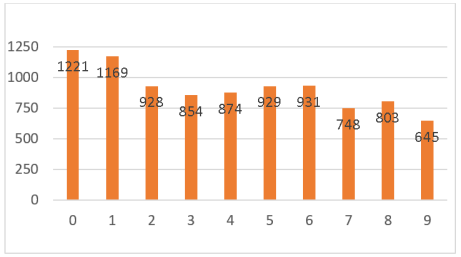
Рис. 6. График распределения цифр коэффициентов
При применении статистических функций к рассчитанному ряду цифр получаются характеристики, представленные в таблице 8.
Таблица 8
Статистические параметры распределения
|
Среднее число вхождений цифры в состав биноминальных коэффициентов |
910,2(10,0 %) |
|
Среднее квадратическое отклонение |
175,5 |
Согласно таблице 8, количество цифр используемых для написания биноминальных коэффициентов первых 50 разложений должно располагаться в интервале 910,2 ± 175,5. В полученных нами верхнюю границу интервала превышают цифры 0 и 1, ниже нижней границы интервала встречается только цифра 9.
Заключение
В ходе проделанной работы мы проанализировали литературные источники и изучили формулу Ньютона, принципы построения треугольника Паскаля, определили основные свойства биноминальных коэффициентов и их математический смысл.
Самостоятельно были получены следующие результаты:
— рассчитаны биноминальные коэффициенты для выборок из 50 элементов и меньше (всего было вычислено 1326 коэффициентов);
— проверено утверждение, что сумма биноминальных коэффициентов для бинома Ньютона степени n равна 2 n ;
— показано, что доля четных биноминальных коэффициентов растет при увеличении степени возведения бинома и меняется от 43,9 % (n=10) до 66,7 % (n=50);
— показано, что самая встречаемая цифра, использующаяся в биноминальных коэффициентах, — 0 (1221 случаев), самая редкая — 9 (645 случаев).
Литература:
- Бродский, Я. С. Статистика. Вероятность. Комбинаторика / Я. С. Бродский. — Москва: ООО «Издательство Оникс», 2008. — 544 с.
- Виленкин, Н. Я. Комбинаторика / Я. Н. Виленкин. — Москва: Наука, 1969. — 328 с.
- Виленкин, Н. Я. Популярная комбинаторика / Я. Н. Виленкин. — Москва: Наука, 1975. — 208 с.
- Виленкин, Н. Я. Индукция. Комбинаторика / Я. Н. Виленкин. — Москва: Просвещение, 1976. — 48 с.
- Макарычев, Ю. Н. Алгебра. 9 класс / Ю.Н Макарычев, Н. Г. Миндюк, К. И. Нешков, И.Е Феоктистов. — 7-е изд. — Москва: Мнемозина, 2008. — 447 с.
- Руэ, Х. Мир математики / Х. Руэ. — Москва: Де Агостини, 2014. — Т. 34. — 144 с.
- Халамайзер, А. Я. Комбинаторика и бином Ньютона / А. Я. Халамайзер. — Москва: Просвещение, 1980. — 32 с.










