В данной статье рассматриваются условия определенного расположения корней при помощи решения задач на квадратные трехчлены с параметрами.
Ключевые слова : квадратные уравнения, неравенства, квадратный трехчлен.
Тема квадратный трехчлен вида ax^2+bx+c занимает довольно большое количество часов на уроках алгебры в школе, ей уделяют много внимания. Ведь знания в этой области необходимы каждому, кто сдает ЕГЭ: задания подобного типа включены в состав и базового, и профильного уровней экзамена для выпускников. И достаточно часто встречаются задачи на решение квадратного уравнения или неравенства с параметром. Именно об этом моя проектная работа. Результаты исследования могут быть применены учителями математики, а также учениками при подготовке к олимпиадам и ЕГЭ по математике базового, профильного уровней. Целью данной работы является при помощи решения задач на квадратные трехчлены с параметрами вывести условия определенного расположения корней.
Квадратным трехчленом называется выражение
ax^2 + bx + c (при этом, а не может быть равным 0 );
Графиком соответствующей функции является парабола.
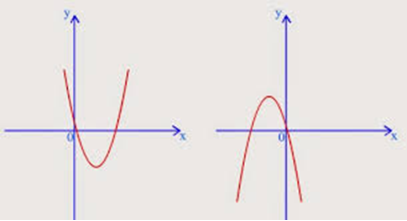
Про дискриминант
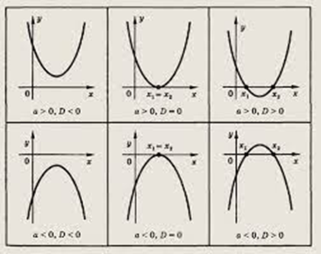
В зависимости от величины дискриминанта D(D=b^2–4ac) возможны различные случаи расположения параболы по отношению к оси абсцисс Ox.
При D > 0 существуют две различные точки пересечения параболы по отношению к оси абсцисс Ox (два различных действительных корня трехчлена)
При D = 0 эти точки совпадают
При D < 0 точки пересечения с осью Ox нет (действительных корней нет); (при а>0 парабола полностью лежит выше Ох ; при а<0 — ниже) [1,2].
Про параметры
Параметр — это коэффициенты при неизвестных/свободные члены, заданные в уравнении или неравенстве не конкретными числовыми значениями, а обозначенные буквами. В квадратном уравнении вида ax^2 + bx + c = 0 есть три параметра — a, b, c. При некоторых значениях параметров уравнение/неравенство имеет 2 корня, при других- 1, при третьих не имеет корней.
Теорема Виета
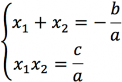
Задача 1
Найти все значения a, при которых оба корня квадратного уравнения
(a+1)x²+2ax+2=0 были бы положительны; были бы отрицательны.
Решение: По условию задачи уравнение должно иметь два корня. Отсюда следует, что D должен быть положителен.
– Существует два случая расположения ветвей параболы: ветви направлены вверх и ветви направлены вниз. Соответственно, выражение (a+1) может быть положительно и отрицательно (нулю равняться не может, т. к. тогда уравнение будет иметь лишь один корень).

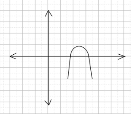
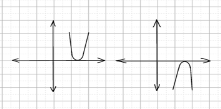
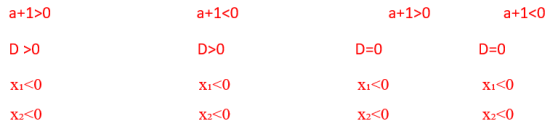
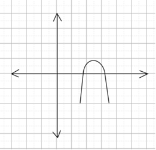
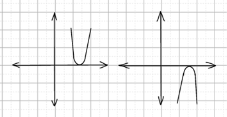
– Для того, чтобы x₁ и x₂ имели одинаковые знаки нужно, чтобы их произведение было положительно (т. к. произведение двух чисел отрицательно только в том случае, если числа разного знака), т. е. свободный член был положителен (по теореме Виета). Здесь это условие выполняется.
– Для положительного знака обоих корней необходимо, чтобы (дополнительно к положительному произведению) их сумма была положительна. Аналогично, для отрицательного знака корней нужна отрицательная сумма.
Значит:
По теореме Виета x₁ x₂=2 и x₁+x₂= -2a
Корни будут положительны, если (2- положительное число) -2a>0 a<0
Корни будут отрицательны, если -2a<0 a>0
Если D>0, то a є (-∞; 1-√3)
Значит, оба корня будут положительны при a є (-∞; 1-√3),
а отрицательны при a є (1+√3; +∞)
Задача решена. После этого мы можем сказать, что вывели условия, при выполнении которых корни любого квадратного уравнения имеют одинаковый знак «+» или «-».
Чтобы корни квадратного трехчлена были действительными и имели одинаковые знаки, необходимо и достаточно выполнение следующих соотношений: D=b²-4ac
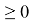

При этом оба корня будут положительными, если дополнительно наложить условия: x₁+x₂= —
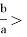
И оба корня будут отрицательны, если x₁+x₂= —
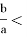
Задача 2
Найти все значения а при которых корни уравнения (a+1)x²+2ax+2=0 действительны и оба больше чем 0,5.
– Корней два — D>0, значит
a
є (-∞; 1-√3) ∪ (1+√3; +∞). Также корни могут совпадать, т. е. D=0 a=1
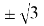
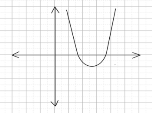
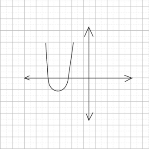
– Если оба корня больше, чем 0,5, то точки (точка) пересечения оси Оₓ параболой находятся (находится) правее. Чем точка с координатами (0,5; 0). Опять же, возможны два случая. Зависящие от первого коэффициента.

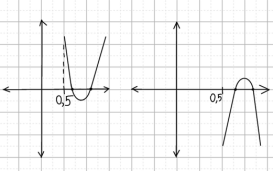
А также:
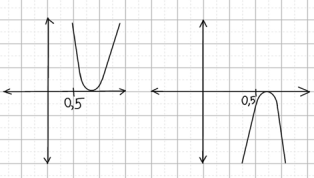
* Рассматривая эти графики можно заметить, что абсцисса вершины параболы находится правее, чем число 0,5.
Значит:
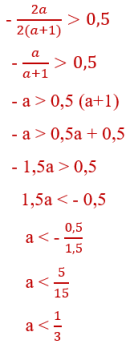
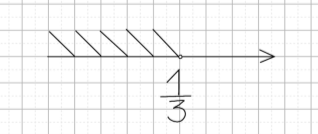
* Далее из рисунка видно, что
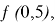
меньше 0, когда a+1<0; и ƒ (𝟎,𝟓)> 0, когда a+1>0.
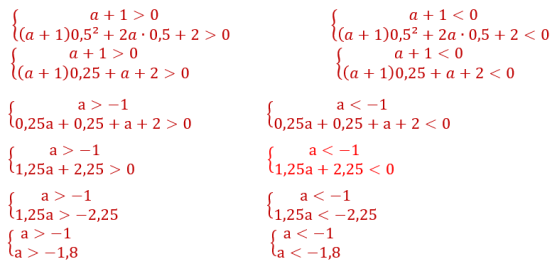
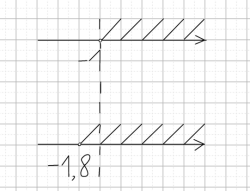
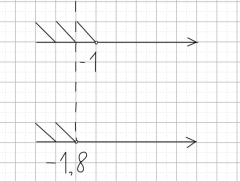
Теперь мы можем найти значения a:
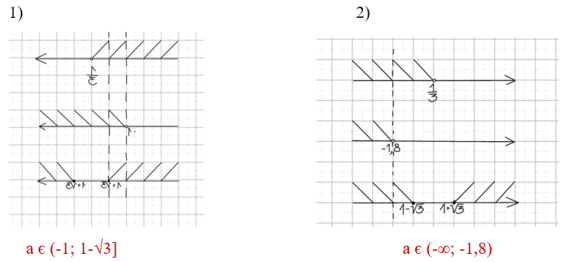
Из решения этой задачи следуют следующие условия, при выполнении которых оба корня квадратного трёхчлена будут больше, чем любое действительное число
xₒ:

Заключение:
В результате работы были даны определения терминов «параметр» и «квадратный трехчлен»; решены четыре задачи и выведены из них три утверждения. Таким образом, благодаря изучению данного раздела, мы научились решать задачи на тему квадратный трехчлен с параметрами и узнали, изучили утверждения, которые нам в этом помогают.
Литература:
- Дробышев Ю. А. Пути формирования знаний о методах решения алгебраических уравнений. — Калуга, 164 с.
- Гашков С. Б. «Квадратный трёхчлен в задачах». Математика (10–11 классы), МЦНМО, 2015, с 21–23.
- Елецких И. А. Математика. Учебное пособие.- Елец, 2016.- 144 с.
- Квон Е. В.,Стукачева М. В. «Квадратный трехчлен в задачах с параметрами» — ННИГУ, 2021, с 76.
- Крамор В. С. «Примеры с параметрами и их решения». Пособие для поступающих в ВУЗы. — М.: АРКТИ, 2001. с 32–36.
- Молодожникова Р. Н. «Квадратный трёхчлен в задачах с параметрами». Метод.указания для учащихся — М,: МАИ, 1996, с 67
- Никитина А. А. «Задачи с параметрами»: методические рекомендации и задачи для самостоятельного решения для учеников 11 класса, ТГУ, 2018, с. 18.
- Седракян Н. М. Неравенства методы неравенства.-М, 2004.256 с.
- Соловьев Ю. П. Неравенства. — М, 2005. 16 с..:с.
- Самаров К. Л. Квадратный трехчлен. Учебное пособие по математике.- М, 2019. 78 с.










