Система диагностики заболеваний на основе нечеткой логики в MATLAB

В статье рассматривается метод постановки наиболее точного диагноза на основе инструментов нечеткой логики. Проанализирована и предложена идея присвоения нечетких переменных интенсивности симптомам. Показаны конкретные примеры созданных систем нечеткой логики.

В медицине часто можно столкнуться с заболеваниями, которые имеют схожие симптомы. А в некоторых случаях у пациентов с одним и тем же заболеванием симптоматика может варьироваться бесконечным множеством раз от пациента к пациенту. Кроме этого, одни и те же симптомы и результаты анализов крови могут быть перекрестными. Именно из-за этого появляется неопределенность в постановке диагноза, и чтобы исключить вероятность ошибки необходимы инновационные технологии, которые могут избавить результат от нечеткости, определяя наиболее точный диагноз. К таким инструментам относится нечеткая логика.

Нечеткая логика на данный момент используется во многих исследованиях в медицине, так как позволяет приходить к точным выводам исходя из нечетких входных данных. Это понятие представляет собой расширение классической теории множеств и формальной логики. Этот концепт был впервые предложен американским ученым Лотфи Заде в 1965 году. [1] Введено также понятие математической теории нечетких множеств, где каждый элемент имеет функцию принадлежности к этому множеству, принимающую значения в интервале [0; 1], а не только 0 или 1, как в классической теории множеств. [2]

Основной характеристикой нечеткого множества является его функция принадлежности. Эту функцию, обозначенную как MFc(x), можно рассматривать как обобщение характеристической функции обычных множеств. Нечеткое множество С представляется в виде упорядоченных пар вида C = {MFc(x)/x}, где MFc(x) принимает значения в диапазоне [0,1]. Значение MFc(x)=0 указывает на отсутствие принадлежности элемента множеству, а значение 1 означает полную принадлежность.

Разработанная модель нечеткой логики, которая основана на статистических данных о заболевании, позволит оказывать помощь пациенту и врачу в постановке диагноза, увеличивая его точность с помощью присвоения нечетких переменных интенсивности симптомов . Главные преимущества методов нечеткой логики проявляются в способности описания лингвистических процессов с использованием словесных логических правил. Следовательно, путем формализации естественно-языковых высказываний типа «Если-то» с использованием теории нечетких множеств можно точно передать любую связь между входными и выходными данными, избегая при этом сложных математических методов дифференциального и интегрального исчисления, которые традиционно используются. [2] Системы были построены в приложении MATLAB.

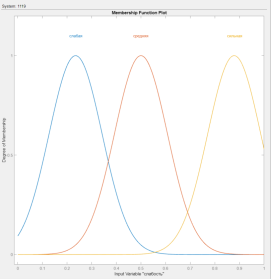
Рис. 1. Описание лингвистической переменной «слабость»

Иными словами, лингвистические переменные будут связаны через правила:

Рис. 2. Схема правил [2]

С помощью них можно будет выполнить операцию нечеткого логического вывода, так как данная база правил будет контролировать определение вероятности отдельно взятого заболевания. Например, заболеванию «свиной грипп» были присвоены следующие лингвистические переменные: «миалгии», «головная боль», «лихорадка», «озноб», «осиплость голоса», «светобоязнь», «тошнота» и «рвота». Также для каждой из них необходимо прописать нечеткие переменные: чаще всего использовались обозначения интенсивности, такие как «слабая», «средняя» и «сильная».

Рис. 3. Описание лингвистической и нечеткой переменных

Сама база правил основывается на схеме, приведенной выше. Например, если каждый из симптомов является «сильным», то вероятность заболевания наивысшая. Если определённые из лингвистических переменных выражены не ярко, то вероятность заболевания соответственно уменьшается и становится средней или наименышей. Однако данная зависимость лингвистических переменных может варьироваться от заболевания к заболеванию, то есть каждая болезнь уникальна и прежде, чем строить для нее систему необходимо собрать всю необходимую справочную информацию касательно постановки диагноза, связанной с интенсивностью симптомов. Так как при одних заболеваниях повышение температуры означает большую вероятность, а для другого — наоборот.

Рис. 4. База правил для заболевания свиной грипп

Это все было необходимо в том числе для создания нечеткого логического вывода, в котором обязательны условия существования хотя бы одного правила для каждого лингвистического терма выходной переменной и тоже самое для входной переменной.

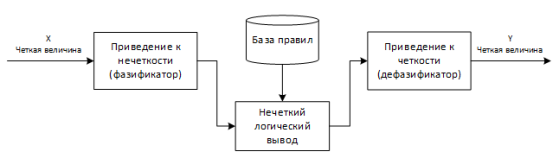
Рис. 5. Система нечеткого логического вывода

В системах был применен дефазификатор Мамдани, так как именно он является наиболее часто используемым инструментом нечеткой логики в медицине. Для получения четкой величины необходимо выбрать интенсивность (зд. нечеткие переменные) каждого симптома в выводе правил в виде числового интервала, которая покажет вероятность данного заболевания относительно интервала, в котором задано заболевание (зд. острый гайморит).

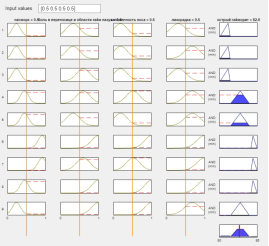
Рис. 6. Вывод правил с одними входными данными

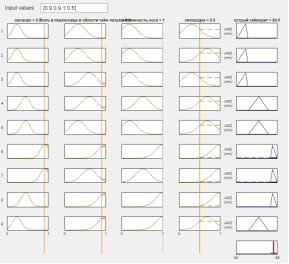
Рис. 7. Вывод правил с отличными входными данными

Данные системы могут стать удобным инструментом уже в настоящее время, который будет дополнительной точкой зрения во время постановки диагноза при нечетких вводных данных. В заключении, были разработаны системы нечеткого вывода, то есть создана модель поддержки принятия решения для диагностики вероятности заболевания при схожих симптомах с другим заболеванием. Предложенный подход позволяет провести обработку большого объема нечетких данных.

1. https://kpfu.ru/staff_files/F850320868/Osnovy_nechetkoj_logiki.pdf (Д. Р. Григорьева, Г. А. Гареева, Р. Р. Басыров//Министерство образования и науки Российской Федерации Набережночелнинский институт (филиал) Федерального государственного автономного образовательного учреждения профессионального образования Казанский (Приволжский) федеральный университет//Основы нечеткой логики) [1]
2. https://web.snauka.ru/issues/2017/06/83588 (Ерёмина В. В., Горожанина Ю. А. Проектирование экспертной системы диагностики на базе нечеткой логики // Современные научные исследования и инновации. 2017. № 6 [Электронный ресурс]) [2]