Задачи на построение одной линейкой

В школьной программе математики содержится изучение задач на построение линейкой и циркулем. В этой статье мы рассмотрим задачи на построение одной линейкой, не используя циркуль как часть решения задачи.

Задание № 1

Даны две параллельные прямые. С помощью одной линейки разделите пополам отрезок, лежащий на одной из данных прямых (рис. 1).

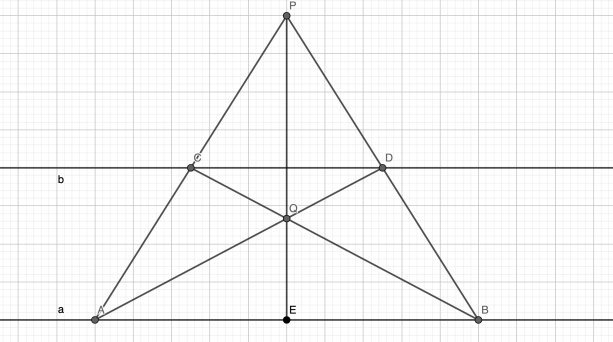
Рис. 1. Построение к заданию № 1

Решение:

1. Возьмём точку P, не лежащую на данных прямых.
2. Соединим точки A и B на прямой с точкой P, получим отрезки AP и BP.
3. Отметим точки пересечений отрезков AP и BP с прямой b, C ∈ AP, D ∈ BP.
4. Соединим точки в отрезки AD и BC.
5. Отметим точку пересечения получившихся отрезков, AD ∩ BC = Q.
6. Соединим точки P и Q, продлим получившийся отрезок до пересечения прямой a в точке E.
7. E — середина отрезка AB -> AE = BE.

Задание № 1 решено.

Задание № 2

Даны две параллельные прямые и отрезок, лежащий на одной из них. Удвойте этот отрезок (рис. 2).

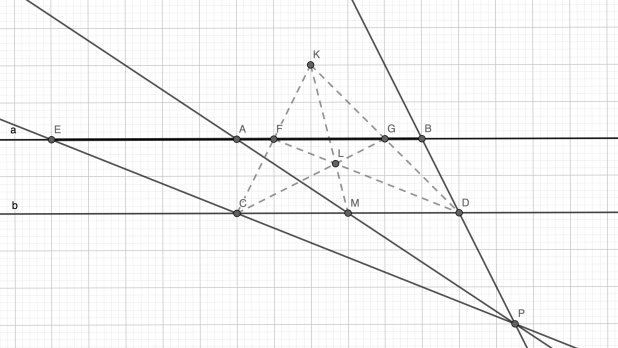
Рис. 2. Построение к заданию № 2

Решение:

1. Возьмём точку K, не лежащую на данных прямых.
2. Соединим точки C и D на прямой с точкой K, получим отрезки CZ и DZ.
3. Отметим точки пересечений отрезков CK и DK с прямой a, F ∈ CK, G ∈ DK.
4. Соединим точки в отрезки CG и DF.
5. Отметим точку пересечения получившихся отрезков, CG ∩ DF = L.
6. Соединим точки K и L, продлим получившийся отрезок до пересечения прямой b в точке M.
7. Продлим отрезки AM и BD до точки пересечения, AM ∩ BD = P.
8. Продлим прямую CP до пересечения с прямой a, CP ∩ a = E.
9. AE = AB -> EB = 2AB.

Задание № 2 решено.

Задание № 3

Даны две параллельные прямые и точка P. Проведите через точку P прямую, параллельную данным прямым (рис. 3).

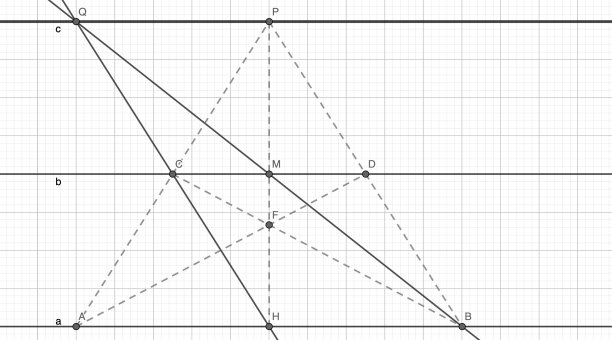
Рис. 3. Построение к заданию № 3

Решение:

1. Соединим точки A и B на прямой с точкой P, получим отрезки AP и BP.
2. Отметим точки пересечений отрезков AP и BP с прямой b, C ∈ AP, D ∈ BP.
3. Соединим точки в отрезки AD и BC.
4. Отметим точку пересечения получившихся отрезков, AD ∩ BC = F.
5. Соединим точки P и F, продлим получившийся отрезок до пересечения прямой a в точке H.
6. Отметим точку M на пересечении отрезка PH и прямой b.
7. Продлим отрезки BD и CH до точки пересечения, BD ∩ CH = Q.
8. Прямая PQ (прямая c) — искомая прямая.

Задание № 4

Дана окружность, её диаметр AB и точка P, не лежащая на окружности. Проведите через точку Р перпендикуляр к прямой AB (рис. 4).

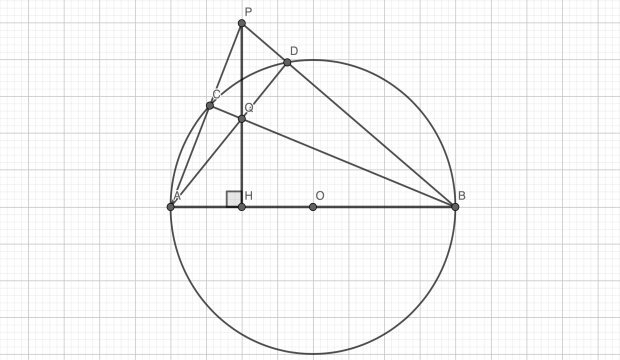
Рис. 4. Построение к заданию № 4

Решение:

1. Отметим точки пересечений отрезков AP и BP с окружностью, C ∈ AP, D ∈ BP.
2. Соединим точки в отрезки AD и BC.
3. Отметим точку пересечения получившихся отрезков, AD ∩ BC = Q.
4. Соединим точки P и Q, продлим получившийся отрезок до пересечения отрезка AB в точке H.
5. PH ⟂ AB.

Задание № 4 решено.

Задание № 5

Дана окружность, её диаметр AB и точка P, лежащая на окружности. Проведите через точку Р перпендикуляр к прямой AB (рис. 5).

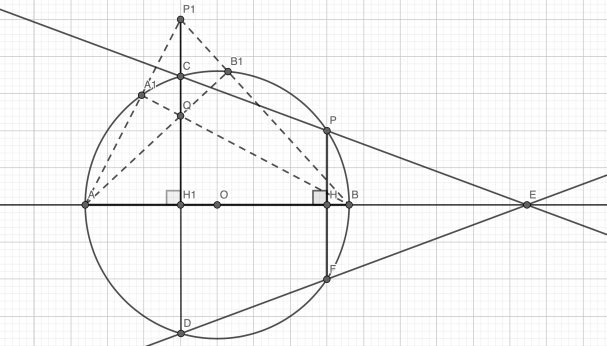
Рис. 5. Построение к заданию № 5

Решение:

1. Возьмём точку P1, не лежащую на окружности.
2. Отметим точки пересечения отрезков AP1 и BP1 с окружностью, A1 ∈ AP1, B1 ∈ BP1.
3. Соединим точки в отрезки AB1 и A1B.
4. Отметим точку пересечения получившихся отрезков, AB1 ∩ A1B = Q.
5. Соединим точки P1 и Q, продлим получившийся отрезок до пересечения отрезка AB в точке H1 -> P1H1 ⟂ AB.
6. Продлим P1H1 до пересечения с окружностью, P1H1 ∩ окр(O;R) = C, P1H1 ∩ окр(O;R) = D.
7. Продлим AB и CP до пересечения, AB ∩ CP = E.
8. Соединим точки D и E, отметим точку пересечения DE с окружностью, DE ∩ окр(O;R) = F.
9. Соединим точки P и F, отметим точку пересечения с отрезком AB, AB ∩ PF = H.
10. PH ⟂ AB.

Задание № 5 решено.

Литература:

1. https://old.mccme.ru//free-books//prasolov/planim/gl8s12.htm