В статье автор рассказывает об интерференции в тонких плёнках, об интерференции в целом, о законе преломления и на этой основе проводит эксперименты для создания ледового комбайна.
Ключевые слова: шероховатость, толщина, интерференция, ледовый комбайн.
Любая, обработанная, даже тщательнейшим образом, поверхность льда, не может быть полностью идеально ровной. Из-за этого на льду образуется шероховатость. Шероховатость — это совокупность микронеровностей, появляющихся на поверхности льда. [2] При этом, шаг неровности, принимаемый в качестве шероховатости, должен быть очень мал, относительно базовой длины всей поверхности.
Вообще, принято выделять три вида шероховатости льда:
– Исходная шероховатость — шероховатость, возникающая в результате технологической обработки льда различными способами.
– Эксплуатационная шероховатость — это приобретаемая в процессе эксплуатации шероховатость в результате износа и рабочего трения.
– Равновесная шероховатость — это вид эксплуатационной шероховатости, который можно воспроизвести в стационарных условиях трения.
Параметры шероховатости определены в ГОСТ 2789–73 «Шероховатость поверхности. Параметры, характеристики и обозначения». Согласно этому документу, выделяют такие показатели шероховатости, как: Ra — это среднее арифметическое значение отклонения поверхности; Rz — это высота неровностей поверхности, снятая в 10 точках; S — это средний шаг местных выступов поверхности; Sm — это среднее арифметическое значение шага неровности; Rmax — это максимальная высота поверхности; tp — это относительная длина поверхности (опорная); р — это уровень сечения поверхности. [6] Проиллюстрируем это на рисунке 1.
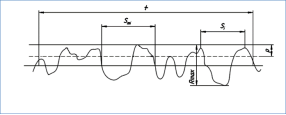
Рис. 1. Показатели шероховатости поверхности льда
При задании шероховатости, как правило, используется параметр среднего арифметического отклонения поверхности (Ra).
Стоит отметить, что именно шероховатость, оказывает наиболее сильное влияние на эксплуатационные характеристики двигателей машин, а также деталей и узлов различного оборудования. Возможно, именно поэтому, точное определение значения шероховатости — одна из самых важных задач метрологии.
Оценка шероховатости может производиться двумя способами: либо поэлементно, путем сравнения отдельных параметров, либо в комплексе, используя сравнительный анализ исследуемого образца с эталоном. Наиболее точным, на данный момент является поэлементный способ, который может быть осуществлен различными методами определения шероховатости: щуповой метод, оптический метод (метод светового свечения и теневой метод, микроинтерференционный метод, растровый метод), метод слепков.
Для оценки шероховатости ледовой поверхности лучше всего подходит оптический метод, реализуемый интеграцией в комбайн толщинометра, работающего в оптическом диапазоне. Этот метод затем будет включён в функции создаваемого ледового комбайна на GPS-управлении для оценки им высоты неровностей льда для подсчёта необходимого объёма воды для заливки и определения высоты ножа. Наряду с оптическим методом применяется более сложный, требующий специального оборудования, метод интерференции.
Физическая основа метода описывается самим явлением интерференции волн.
Интерференция — это взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. [2] Интерференцией волн называется явление, возникающее при сложении двух волн, вследствие которого наблюдается усиление или ослабление результирующих колебаний в различных точках пространства. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и постоянную разность фаз их колебаний. Такие волны называются когерентными.
При отражении света от двух границ воздушного зазора между выпуклой поверхностью линзы и плоской пластиной возникают интерференционные кольца — кольца Ньютона. В основе исследования толщины льда лежит изучение интерференции в тонких плёнках.
При падении света на прозрачную диэлектрическую пластинку он частично преломляется, а частично отражается от обеих её поверхностей. Рассмотрим падение параллельного пучка света из вакуума или воздуха на плоскопараллельную прозрачную пластинку толщиной d. Угол падения (и угол отражения) равен α, а угол преломления — β. Показатель преломления вещества пластинки равен n. В точке А волна частично преломляется (луч АВ), а частично отражается (луч АС). Какая доля энергии отражается, а какая преломляется, зависит от соотношения показателей преломления сред и угла падения, для стекла (показатель преломления 1,5) при лобовом падении волны из вакуума или воздуха отражается около 4 % падающей энергии, а остальные 96 % преломляется. Преломлённая волна, в свою очередь, падает на нижнюю грань пластинки, и в точке В волна снова делится на две. То же самое происходит в точке D и т. д. В итоге от пластинки отражаются две волны (лучи 1 и 2), и также будут две преломлённые волны. Вообще говоря, будут происходить и дальнейшие отражения и преломления, но энергия и амплитуда этих последующих волн ничтожно мала. Проиллюстрируем это на рисунке 2.
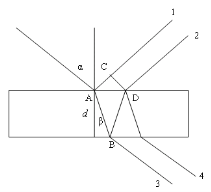
Рис. 2. Падение параллельного пучка света из вакуума или воздуха на плоскопараллельную прозрачную пластинку толщиной d
На основе теоретической части мы можем перейти к практической части, основанной на более упрощённом методе исследования. Явлении преломления света в пластинах.
Проведём опыт. С помощью ледоруба отрежем от льда кусок небольшой льдины. Важно, чтобы лёд был ровный для более точных измерений. Затем, при помощи бытового лазера, направим на льдину луч, то есть посветим на льдину лазером. Можно увидеть, что луч проходит через льдину и отражается от неё. Образуется небольшая точка. Тем самым на льдине появляются две точки от луча лазера. Первая точка — это точка входа (точка, в которую попал первоначальный луч лазера), а вторая точка — это точка выхода (точка выхода отразившегося луча). После этого отметим эти точки. Далее с помощью линейки высчитаем расстояние между этими точками. Это расстояние будет равно толщине льдины. Таким образом, с помощью лазера и линейки мы можем высчитать толщину льда. Проиллюстрируем это на рисунке 3.

Рис. 3. Измерение толщины куска небольшой льдины
На основе этого опыта мы можем измерить толщину льда на ледовой площадке. С помощью лазера в определённом месте ледовой площадки просветим лёд и увидим отражённую точку. Зафиксируем эти точки и измерим расстояние между ними. Мы получим толщину льда в этом месте. Такое исследование мы проделаем несколько раз в разных местах ледовой площадки. Таким образом, в разных местах расстояние между двумя точками разное, следовательно толщина льда не одинакова, следовательно, на льду есть шероховатость. Эта шероховатость появляется впоследствии срезания льда коньками (при катании) и ручной заливки. Таким образом мы проверили, что такой метод исследования шероховатости льда работает. Он будет включён в программу создаваемого нами ледового комбайна на GPS-управлении. Проиллюстрируем это на рисунке 4.

Рис. 4. Измерение толщины льда на ледовой площадке
На основе этого проведём эксперимент и составим таблицу. Также с помощью лазера и линейки измерим толщину льда в разных местах хоккейной площадки до игры. Сначала измерим толщину льда для первого места. Найдём расстояние между двумя точками, оно примерно равно 50,8 мм. По закону Снелиуса:

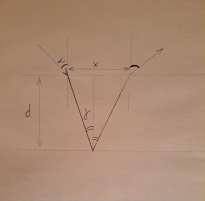
Рис. 5. Измерение толщины льда, где d — толщина льда, x — расстояние между двумя точками
Примем значение толщины льда за d. Далее, исходя из прямоугольного треугольника мы получаем формулу
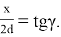
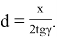
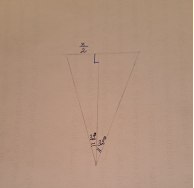
Рис. 6. Измерение толщины льда
Итак, толщина льда в первом месте хоккейной площадки примерно равна 41 мм. Аналогично измеряем толщину льда в других местах хоккейной площадки. Зафиксируем эти показания в таблице. Затем пройдёт хоккейный матч, в котором играют две команды (по 6 человек в каждой команде) продолжительностью 60 минут (3 периода по 20 минут + 2 перерыва по 15 минут). Перерывы не учитываются, так как во время перерывов игроки не катаются на льду. После матча повторно замерим и вычислим толщину льда в этих же местах хоккейной площадки аналогичным способом. Зафиксируем результаты. Запишем их в таблицу. Далее, зная толщину льда до игры и толщину льда после игры, посчитаем толщину льда, которая была срезана хоккеистами во время игры. Исходя из 5 разных значений, посчитаем среднее значение. Сведём данные нашего исследования в таблице 1.
Таблица 1
Нахождение средней толщины срезанного льда на хоккейной площадке
|
Место площадки, № |
Толщина льда до игры, мм |
Толщина льда после игры, мм |
Толщина срезанного льда, мм |
|
1 |
41 |
39,3 |
1,7 |
|
2 |
40 |
38,2 |
1,8 |
|
3 |
41,5 |
39,9 |
1,6 |
|
4 |
42 |
40,35 |
1,65 |
|
5 |
39,5 |
37,65 |
1,85 |
|
Среднее значение |
40,8 |
39,02 |
1,78 |
Можно заметить, что толщина льда в разных точках площадки неодинакова, есть небольшая погрешность, которая появилась в результате ручной заливки.
Таким образом мы посчитали, что в среднем за 60 минут игры срезается 1,78 мм льда.
Мы знаем, что в среднем размеры хоккейной площадки таковы: длина — 60 м, ширина — 30 м. Также мы посчитали толщину, то есть высоту льда. Она равна 1,78 мм = 0,0078 м.
Мы знаем формулу объёма: V=abc. По этой формуле мы можем посчитать объём срезанного льда, подставив известные нам величины в эту формулу: V = 60 м * 30 м * 0,0078 м = 14,04 м³ ≈ 15 м³. Таким образом, объём воды, необходимый для восстановления срезанного объёма льда примерно равен 15 м³ или 15000 л. Эта функция в дальнейшем будет включена в программу комбайна и будет использована для установки на комбайн бака с необходимым объёмом. Проиллюстрируем это на рисунке 5.

Рис. 7. Нахождение объёма срезанного льда
На основании этого мы можем сделать выводы.
- По первому опыту мы выяснили, что с помощью бытового лазера и линейки можно посчитать толщину льдины.
- Исходя из первого опыта мы провели эксперимент, в котором выяснили, что таким же образом мы можем посчитать толщину льда на хоккейной площадке. Исходя из этого мы нашли среднюю толщину льда на хоккейной площадке.
- Зная среднюю толщину льда, мы нашли объём льда, срезаемого во время игры. Исходя из этого мы посчитали, какой объём воды необходим для восстановления этого льда.
- В дальнейшем, при создании ледового комбайна нам предстоит написать программу, которая будет определять объём необходимой воды для восстановления льда на основании его срезанной толщины.
Литература:
- Грачёв А. В., Погожев В. А., Боков П. Ю. Физика 9 класс: учебник. Изд-во «Просвещение», 2021
- Громов С. В. Энциклопедия элементарной физики. Книга для учащихся. Изд-во «Просвещение», 2007
- Луис А. Блумфилд. Как всё работает. Законы физики в нашей жизни. Изд-во Политекс, 2016
- Роджерс Э. Физика для любознательных. М.: Изд-во Мир, 1972
- Тарасов Л. В. Физика в природе — М.: Просвещение, 1988
- Яворский Б. М., Пинский А. А. Основы физики. М.: Изд-во «Наука», 1974











