1. Мультиномиальная теорема
Рассмотрим полином Ньютона [1] — выражение вида
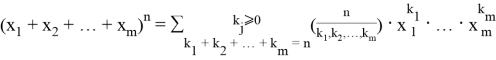
где
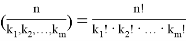
Здесь сумма берется по всем неотрицательным целым индексам
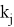
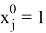
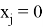
При
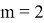
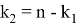
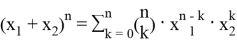
где
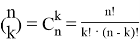
Докажем формулу для полинома Ньютона (мультиномиальную теорему) методом математической индукции по
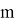
База индукции.
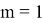
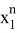
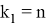
Шаг индукции.
Предположим, что мультиномиальная теорема верна для
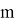
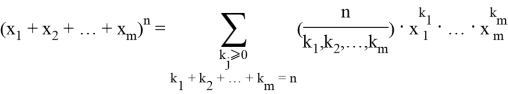
Надо доказать утверждение для
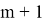
Начнем доказательство.
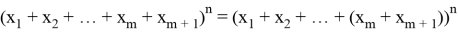
=
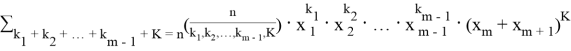
Применяя биномиальную теорему к последнему множителю получаем:
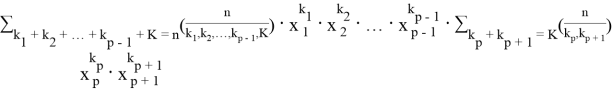
=
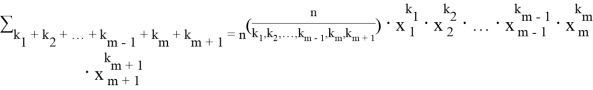
Что завершает шаг индукции.
Последнее следует из того, что
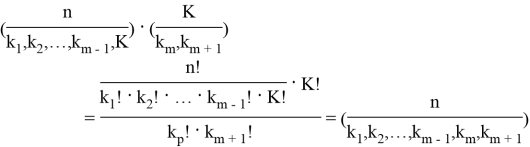
2. Поиск наибольшего члена разложения бинома Ньютона
Рассмотрим бином Ньютона:
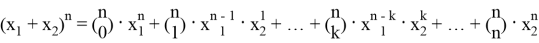
Пусть
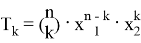
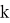
Тогда для наибольшего члена разложения имеем:
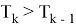
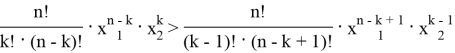
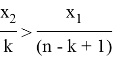
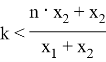
Также для наибольшего члена разложения имеем:
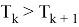
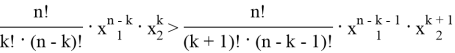
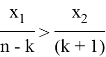
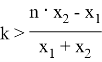
Окончательно,
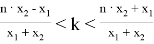
Так как интервал Δ нахождения номера k наибольшего члена разложения
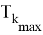
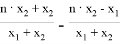
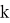
Данное значение
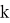
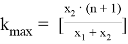
Тогда значение наибольшего члена разложения равно:
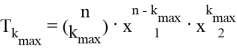
Следует заменить, что если значения выражений
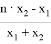
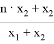
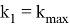
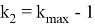
По приведенным выше формулам также, например, для выражения
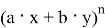
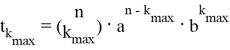
Пример № 1.
Найти наибольший коэффициент разложения
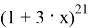
Решение 1.
Общий член данного разложения есть
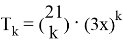
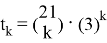
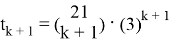
Имеем
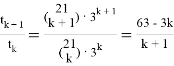
Чтобы найти, где коэффициенты возрастают, решаем
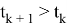
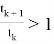
Имеем
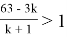
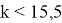
Так как
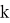
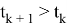
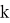
Последовательность коэффициентов возрастает от
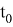
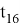
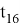
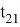
Следовательно,
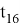
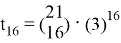
Решение 2.
Воспользуемся формулой (4):
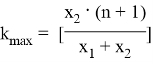
Имеем,
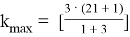
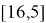
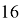
Наибольший коэффициент:
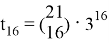
Пример № 2.
Найти наибольший коэффициент разложения
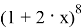
Решение.
Воспользуемся формулой (4):
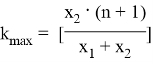
Имеем,
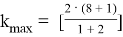
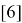
Наибольшие коэффициенты:
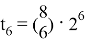
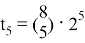
3. Поиск наибольшего члена разложения полинома Ньютона
Рассмотрим полином Ньютона
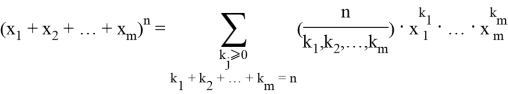
Пусть
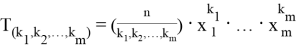
Тогда имеем систему неравенств для
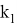
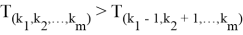
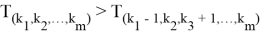
...
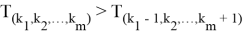
А также
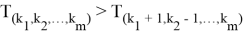
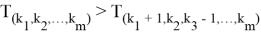
...
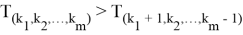
Расписывая неравенство (6) получаем:
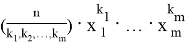
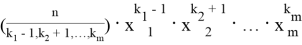
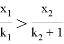
Аналогично из неравенства (7) следует
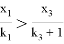
C другой стороны из неравенства (8) следует
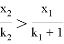
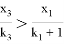
Похожим образом выписывая неравенства для
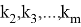
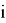
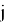
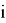
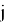

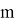
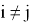
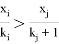
3.1. Алгоритм нахождения наибольшего члена разложения полинома Ньютона.
В данной задаче будем рассматривать положительные слагаемые в полиноме Ньютона. Расположим их, для удобства, в порядке увеличения:
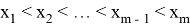
На основании результатов раздела 2 положим:
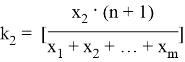
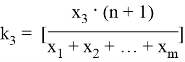
...
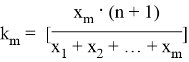
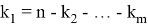
Вычислим

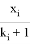
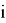

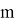
Если выполняется условие
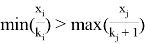
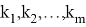
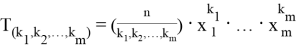
Если условие
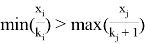
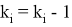
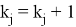
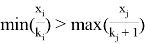
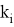
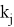
Отдельно следует рассмотреть случай, когда возникает равенство
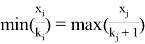
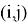
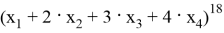
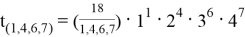
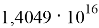
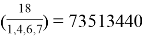
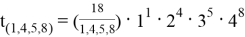
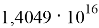
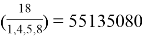
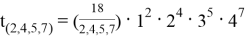
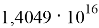
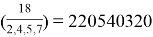
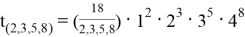
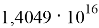
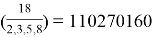
Условия возникновения данного равенства предполагается рассмотреть в последующих работах.
Пример № 3.
Найти наибольший член разложения:
а)
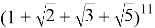
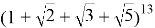
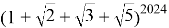
Решение.
Длярешения данной задачи в программе Microsoft Excel были написаны выведенные выше формулы, которые позволили получить следующие результаты:
Для
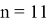
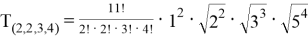
Для
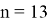
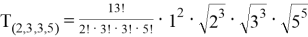
Для
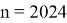
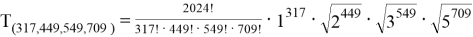
Литература:
- https://ru.wikipedia.org/wiki/ Бином_ Ньютона









