Изучали образование перколяционных кластеров c использованием модели пористой структуры, которая может быть использована как модель чувствительных элементов для газовых адсорбционных датчиков, в сравнении с моделями на квадратной и треугольной решетках.
Ключевые слова: перколяционные кластеры, квадратная решетка, треугольная решетка, пористая структура.
С конца семидесятых годов прошлого века стала широко использоваться теория перколяции («перколяция» означает «протекание, просачивание») для объяснения разнообразных явлений [1–5]. В последнее время теории перколяции нашли своё широкое применение в различных сферах деятельности: компьютерной графике, физике, технике, биологии, медицине, экономике и т. д. Например, перколяция применяется для оценки надежности компьютерных сетей, в медицине — для анализа распространения эпидемий, в химии — для описания процессов гелирования, т. е. связывания молекул в макромолекулы, в биологии — для моделирования распространения лесного пожара [4], а также для моделирования распространения пламени в сельской местности.
В качестве объектов исследованиядля построения моделей перколяционных кластеров были выбраны: квадратная решетка; треугольная решетка; пористая структура. Т. к. теория перколяции тесно связана со случайными числами (величинами, о которых известно, какие значения они принимают, но неизвестно, какие именно значения они примут в конкретном случае), то работали со случайными числами, которые получали с помощью онлайн-генератора случайных чисел (или рандомайзера). В качестве иллюстрирующего примера на рис.1 (слева) приведены 100 случайных чисел (от 1 до 6), покрашенных в желтый (значения от 1 до 3) и голубой цвет (значения от 4 до 6). Пример образования перколяционного стягивающего кластера представлен на рис. 1 справа.

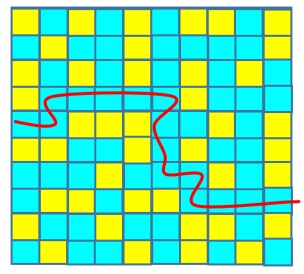
Рис. 1. Образование перколяционного кластера на квадратной решетке (при 59 голубых ячейках из 100 ячеек)
Таким образом, в работе исследовали модели перколяционных кластеров на квадратной решетке из 100 ячеек (рис. 1 справа), треугольной решетке из 100 ячеек (рис. 2 слева), и пористой структуре из 120 ячеек (рис. 2 справа). В таблице 1 приведены результаты десяти экспериментов на треугольной решетке из ста ячеек, десяти экспериментов на квадратной решетке из ста ячеек и десяти экспериментов на модели пористой структуры из ста двадцати ячеек. Находили среднее арифметическое значение количества голубых ячеек, при котором возникает перколяционный кластер. В работе выявлено, что перколяционный кластер на треугольной решетке возникает при половине голубых ячеек, перколяционный кластер на квадратной решетке возникает, когда голубых ячеек больше половины. В сравнении с квадратной решеткой перколяционный кластер для модели пористой структуры возникает при большем количестве голубых ячеек (рис. 3).
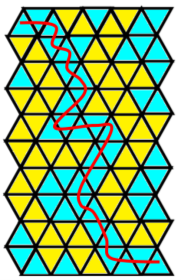
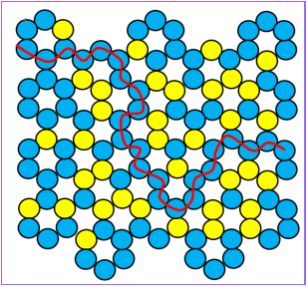
Рис. 2. Пример образования перколяционного кластера на треугольной решетке и на модели пористой структуры
Таблица 1
Проведение 30 экспериментов на трех решетках
|
Номер эксперимента |
Треугольная решетка из 100 ячеек |
Квадратная решетка из 100 ячеек |
Модель пористой структуры из 120 ячеек |
|
Количество голубых ячеек |
|||
|
1 |
45 |
59 |
78 |
|
2 |
54 |
60 |
84 |
|
3 |
53 |
58 |
82 |
|
4 |
46 |
56 |
80 |
|
5 |
48 |
62 |
78 |
|
6 |
52 |
63 |
82 |
|
7 |
49 |
64 |
80 |
|
8 |
50 |
59 |
82 |
|
9 |
52 |
58 |
78 |
|
10 |
51 |
61 |
76 |
|
Среднее значение |
50 |
60 |
80 |
Модель перколяционного кластера на квадратной решетке может быть использована для моделирования распространения лесного пожара, а также для моделирования распространения пламени в сельской местности.
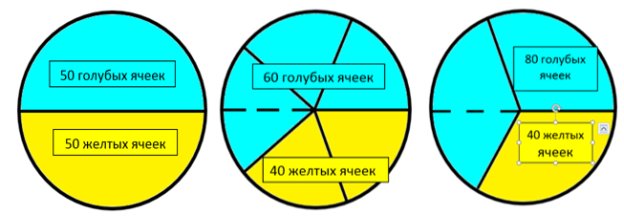
Рис. 3. Количество ячеек, которое должно быть в системе, чтобы возник перколяционный кластер: слева — для треугольной решетки, в середине — для квадратной решетки, справа — для модели пористой структуры
Для моделирования распространения лесного пожара предполагают, что лес посажен в виде квадратной решётки и что огонь может перекинуться на ближайшие деревья. Чтобы обезопасить лес от разрушительных пожаров, вырубают случайно выбранные деревья. Решается задача, какая минимальная часть деревьев должна быть вырублена, чтобы лесного пожара не было.
Модель перколяционной пористой структуры может быть использована как модель чувствительных элементов для газовых адсорбционных (адсорбция — поглощение газа поверхностью твердого тела) датчиков на основе наноматериалов для улучшения их характеристик (чувствительности и селективности, т. е. избирательности). Чувствительный элемент для современных газовых адсорбционных датчиков, разрабатываемый учеными в настоящее время, может быть сформирован в виде пористой наноструктуры, состоящей из частиц двух видов, размеры которых так малы, что их можно наблюдать только с помощью специальных микроскопов. Частицы одного типа отвечают за чувствительность газового датчика, а частицы другого типа за улучшение сцепления с подложкой, на которую наносится газочувствительный пористый слой.
Работа выполнена по направлениям «Проектная деятельность» и «Микро- и наноэлектроника» в рамках создания и функционирования центра цифрового образования детей «ИнфинITи» (на базе ГБОУ СОШ № 435 Курортного района Санкт-Петербурга), созданного Комитетом по образованию Санкт-Петербурга в рамках регионального и федерального проектов «Цифровая образовательная среда» национального проекта «Образование».
Литература:
- Эфрос А. Л. Физика и геометрия беспорядка. (Библиотечка «Квант», выпуск 19). М.: Из-во «Наука», 1982. 265 с.
- Тарасевич Ю. Ю. Перколяция. Теория, приложения, алгоритмы. Либроком. 2018. 112 с.
- Lin J., Zhang W., Chen H., Zhang R., Liu L. Effect of pore characteristic on the percolation threshold and diffusivity of porous media comprising overlapping concave-shaped pores. Transfer. 2019. V. 138. P. 1333–1345.
- Астафьев. С. А., Лысенко Д. Ю., Широков А. С. Моделирование процесса распространения лесного пожара с применением теории перколяции. Изв. ВУЗОВ. Приборостроение. 2012. T. 55, № 6. С. 70–74.
- Sharma A., Eadi S. B., Noothalapati H., Otyepka M., Lee H.-D., Jayaramulu K. Porous materials as effective chemiresistive gas sensors. Chem. Soc. Rev.2024. V. 53. P. 2530–2577.










