Площади треугольников с координатами из последовательных чисел на декартовой плоскости



Введение

На уроках математики в 5-м классе у нас было задание посчитать площади треугольников на Декартовой плоскости. Эта задача нередко достаточно сложная, ведь вершины фигуры могут очень сильно отстоять друг от друга. Тогда найти её площадь проще всего через операции с координатами вершин.

В начале работы я рассматривала площади треугольников с координатами из последовательных чисел из разных числовых последовательностей. Затем, с помощью написанных программ на Python проводила численные эксперименты. А после этого переходила к строгой математической формулировке гипотез и доказательств на бумаге. В статье порядок повествования изменен: сначала даны формулировки гипотез и доказательства. А лишь в конце представлены коды программ и их результаты.

Формула площади треугольника на Декартовой плоскости

Если посмотреть, как считается площадь треугольника через координаты, то можно заметить алгоритм, работающий при всех случаях. Сначала нужно вписать фигуру в прямоугольник, диагональ которого будет стороной треугольника, то есть две вершины треугольника будут находиться в противоположных углах четырехугольника. Тогда третья вершина будет в одном из треугольников, составляющих прямоугольник. Потом из половины четырехугольника нужно вычесть 2 прямоугольных треугольника и квадрат (его стороны могут быть равны 0).

Тогда при , ,

:

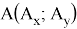
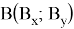
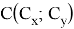
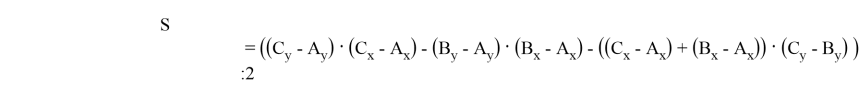
В зависимости от того тупой угол будет лежать в верхней части от большей стороны или в нижней, площадь получится либо положительной либо отрицательной по формуле. Но нам интересно абсолютное значение, т. к. минус появляется из-за предположения о размещении треугольника в одной части.

Определения

Числа Фибоначчи — элементы числовой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны 1 и 1, а каждое последующее число равно сумме двух предыдущих чисел.

Числа Люка — элементы числовой последовательности: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, …, в которой первые два числа равны 2 и 1, а каждое последующее число равно сумме двух предыдущих чисел.

Числа Пелля — элементы числовой последовательности: 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860..., в которой первые два числа равны 1 и 2, а каждое последующее число равно сумме удвоенного предыдущего и предшествующего предыдущему.

Гипотеза 1: числа Фибоначчи

Однажды мне встретилось задание посчитать площадь треугольника с координатами A(1;1), B(2;3), C(5;8). Можно заметить, что его координаты — это последовательные числа Фибоначчи, и его площадь равна

((8–1)

(5–1) — (3–1) (2–1) — ((5–1) + (2–1)) (8–3)) / 2 = 0,5.

Также я проверила площади треугольников с координатами A(1;2), B(3;5), C(8;13); A(2;3), B(5;8), C(13;21); A(8;13), B(21;34), C(55;89), они тоже оказались равными 0,5.

Теорема 1 : площадь любого треугольника с координатами из последовательных чисел Фибоначчи равна 0,5.

Доказательство гипотезы

Так как каждое число Фибоначчи — это сумма двух предшествующих ему, то при , , :

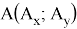
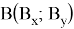
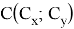
Cy — By = Cx; Cy — Ay = Cx + Bx; By — Ay = Bx; Cx — Ax = Ay + By; Cx — Bx = By; Bx — Ax = Ay.

Тогда формулу можно представить через Bx и By: = 2

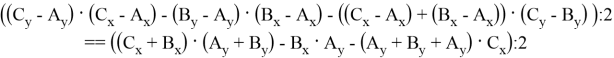
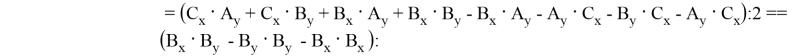
Докажем по индукции, что для любых двух последовательных чисел Фибоначчи , начиная с третьего и четвертого 2 = 0,5

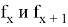
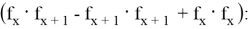
База:

A(1;1), B(2;3), C(5;8); (3 3 + 2 2) 2 = 0,5

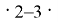
Предположение индукции:

Пусть для треугольника с координатами:

, ,

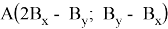
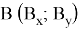
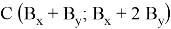
площадь равна 0,5.

Шаг индукции:

Тогда найдем площадь треугольника с координатами:

,

,

: 2 = + 2

+

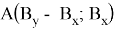
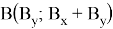
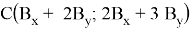
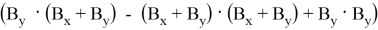
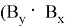
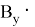
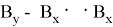
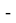
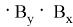
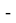
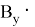
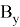
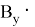
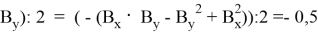
Следовательно, площадь треугольника, заданного координатами из последовательных чисел Фибоначчи, равна 0,5 по предположению индукции.

Получается S = : 2 = 0,5.

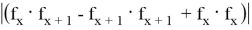
Так как для ( x +1) случая площадь та же, то и для всех таких треугольников площадь равна 0,5.

Гипотеза доказана

Также ниже представлена программа на Python, вычисляющая площади 300 разных треугольников с координатами из чисел Фибоначчи и ее результат.

КОД:

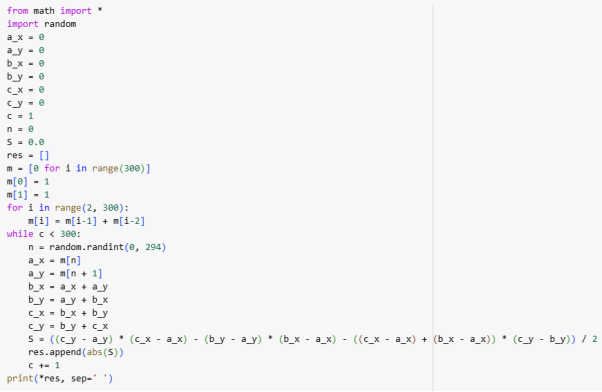
РЕЗУЛЬТАТ:

0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 … 0.5

Гипотеза 2: числа Люка

После доказательства первой гипотезы 1, я решила проверить другие последовательности. Одной из них оказалась последовательность Люка. Она начинается с 2 и 1, а дальше, как и в последовательности Фибоначчи, каждое следующее число равно сумме двух предыдущих. 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123 и так далее. Площади первых пяти треугольников оказались равными 2,5.

Гипотеза 2 : площадь любого треугольника с координатами из последовательных чисел Люка равна 2,5.

Доказательство гипотезы

Так как каждое число Люка — это сумма двух предшествующих ему, то при

, ,

:

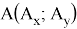
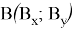
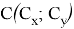
Cy — By = Cx; Cy — Ay = Cx + Bx; By — Ay = Bx; Cx — Ax = Ay + By; Cx — Bx = By; Bx — Ax = Ay.

Тогда формулу можно представить через : = 2

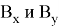
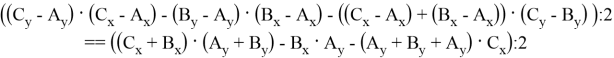
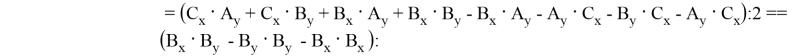
Докажем по индукции, что для любых двух последовательных чисел Люка, , начиная с третьего и четвертого, 2 = 2,5

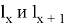
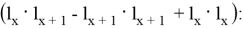
База:

A(2;1), B(3;4), C(7;11); (3

4 + 3 3) 2 = 2,5

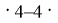
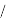
Предположение индукции:

Пусть для треугольника с координатами:

, ,

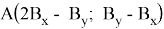
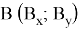
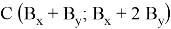
площадь равна 2,5.

Шаг индукции :

Тогда найдем площадь треугольника с координатами:

, ,

: 2 = + 2

+ )): 2 = -2,5

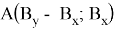
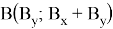
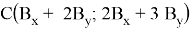
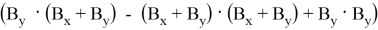
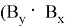
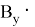
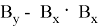
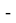
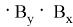
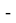
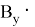
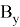
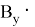
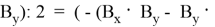
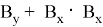
Следовательно, площадь треугольника, заданного координатами из последовательных чисел Люка, равна 2.5 по предположению индукции.

Получается S = : 2 = 2,5.

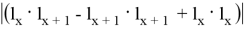
Так как для ( x +1) случая площадь та же, то и для всех таких треугольников площадь равна 2,5.

Гипотеза доказана

Также ниже представлена программа на Python, вычисляющая площади 300 разных треугольников с координатами из чисел Люка, и ее результат.

КОД:

РЕЗУЛЬТАТ:

2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 … 2.5

Гипотеза 3: числа Пелля

Также я рассмотрела площади треугольников с координатами из последовательных чисел Пелля. Первые несколько чисел из этой последовательности 1, 2, 5, 12, 29, 70, 169, в ней каждое следующее число сумма удвоенного предыдущего и предшествующего предыдущему. Площади первых пяти треугольников оказались равными 4

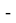
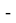
Гипотеза 3 : площадь любого треугольника с координатами из последовательных чисел Пелля равна 4.

Доказательство гипотезы

При , , :

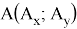
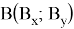
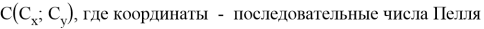
Cy — By = 2Cx; Cy — Ay = 2Cx + 2Bx; By — Ay = 2Bx; Cx — Ax = 2Ay + 2By; Cx — Bx = 2By; Bx — Ax = 2Ay.

Тогда формулу можно представить через B _x и B _y :

=

: 2

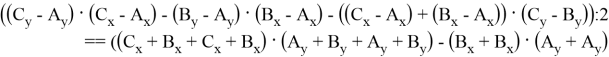
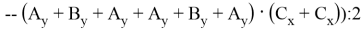
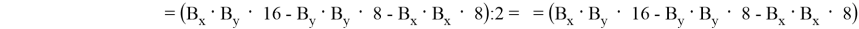
Докажем по индукции, что для любых двух последовательных чисел Пелля, , начиная с третьего и четвертого, 2 = 4

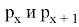
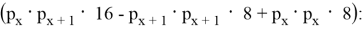
База:

A(1;2), B(5;12), C(29;70); (5 12 12 12 + 5

5 ) 2 = 4

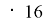
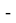
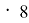
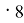
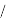
Предположение индукции:

Пусть для треугольника с координатами:

, ,

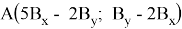
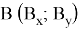
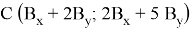
площадь равна 4.

Шаг:

, ,

: 2 )): 2 = -4

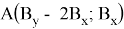
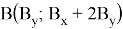
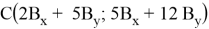
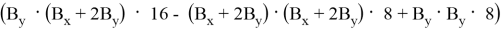
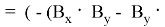
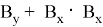
Следовательно, площадь треугольника, заданного координатами из последовательных чисел Пелля, равна 4 по предположению индукции.

Получается S = : 2 = 4.

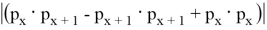
Так как для ( x +1) случая площадь та же, то и для всех таких треугольников площадь равна 4.

Гипотеза доказана

Также ниже представлена программа на Python, вычисляющая площади 300 разных треугольников с координатами из чисел Пелля и ее результат.

КОД:

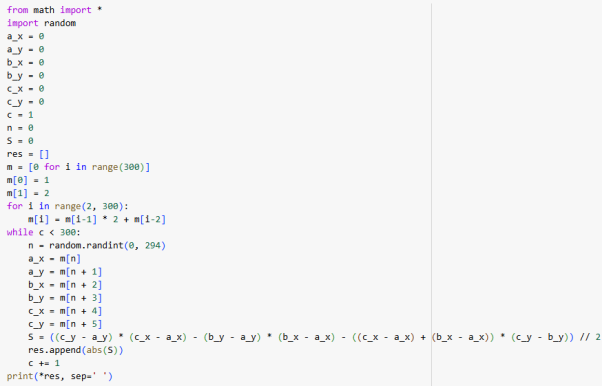
РЕЗУЛЬТАТ:

4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 … 4

Результаты

В ходе исследования я доказала, что:

1. Треугольники с координатами из последовательных чисел Фибоначчи всегда имеют площадь 0,5;
2. Треугольники с координатами из последовательных чисел Люка всегда имеют площадь 2,5;
3. Треугольники с координатами из последовательных чисел Пелля всегда имеют площадь 4.

Выводы

В ходе исследования я рассмотрела треугольники с координатами:

1. из чисел Фибоначчи;
2. из чисел Люка;
3. из чисел Пелля.

Для каждой группы была найдена площадь.

Для каждого случая было:

— сформулирована гипотеза;

— доказана гипотеза;

— проведен численный эксперимент.

Литература:

1. Онлайн-энциклопедия целочисленных последовательностей https://oeis.org/?language=russian
2. Числа Пелля https://ru.m.ruwiki.ru/wiki/ %D0 %A7 %D0 %B8 %D1 %81 %D0 %BB %D0 %BE_ %D0 %9F %D0 %B5 %D0 %BB %D0 %BB %D1 %8F
3. Последовательность Люка https://ru.m.wikipedia.org/wiki/ %D0 %9F %D0 %BE %D1 %81 %D0 %BB %D0 %B5 %D0 %B4 %D0 %BE %D0 %B2 %D0 %B0 %D1 %82 %D0 %B5 %D0 %BB %D1 %8C %D0 %BD %D0 %BE %D1 %81 %D1 %82 %D1 %8C_ %D0 %9B %D1 %8E %D0 %BA %D0 %B0
4. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В./ Математика. 5 класс: учеб. для общеобраз. учреждений / М.: Просвещение, 2012