Геометрические построения имеют богатую историю и восходят к Евклиду: ещё в самой первой задаче «Начал» (300 г. до н. э.) читателю предлагается задание на построение. Такие упражнения позволяют людям научиться искать пути решения задач и анализировать различные ситуации. В наше время геометрические построения имеют и прикладной характер — они широко используются инженерами в черчении.
Будем предполагать, что у нас имеется циркуль и линейка без делений. Задачи на построение предполагают три этапа:
1) построение и описание хода действий;
2) доказательство;
3) выяснение условий существования решения задачи.
Рассмотрим две задачи и проиллюстрируем выполнение геометрических построений.
Задача 1.
Построить с помощью циркуля и линейки отрезок, равный данному отрезку
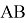

Рис. 1.
Построение.
1) Поставим точку
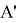
2) С помощью циркуля измеряем отрезок
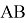
3) С помощью циркуля строим окружность
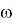
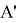
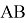
4) С помощью линейки проводим из точки
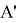
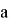
5) Обозначим точкой
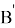
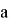
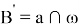
6) Отрезок
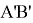
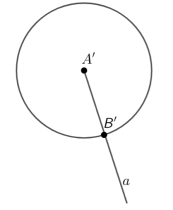
Рис. 2.
Доказательство.
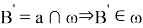
Тогда по определению окружности
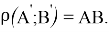
Таким образом,
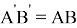
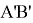
Условия существования решения задачи.
Решение данной задачи существует всегда. Всегда можно с помощью циркуля построить окружность данного радиуса с центром в некоторой точке, с помощью линейки провести луч с началом в некоторой точке, причём луч обязательно пересечёт окружность, если его начало лежит внутри окружности. Тогда каждый шаг нашего построения всегда имеет место.
Задача 2. Построить треугольник по трём сторонам, длины которых равны длинам отрезков
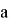
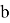
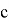
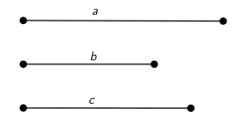
Рис. 3.
Построение.
1) Построим
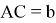
2) Построим с помощью циркуля окружность
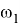
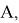
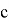
3) Построим с помощью циркуля окружность
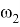
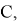
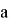
4) Обозначим
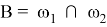
5) Треугольник
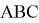
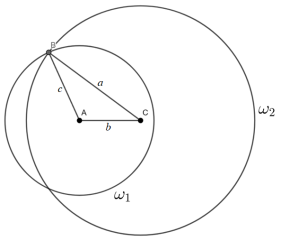
Рис. 4.
Доказательство.
По построению
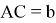
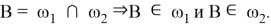
По построению
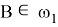
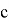
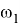
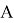
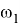
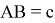
По построению
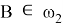
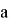
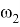
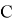
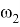
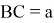
Таким образом, треугольник
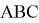
Условия существования решения задачи.
Из нашего построения видно, что условиями существования треугольника
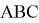
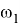
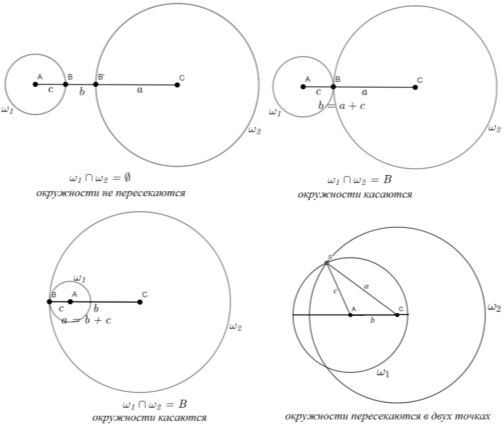
Рис. 5.
Рассмотрев радиусы
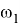
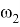
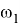
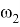
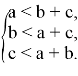
Литература:
- Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др., Геометрия. 7–9 классы: учеб. для общеобразоват. организаций, 8-е изд., М.: Просвещение, 2018, 383 с.
- Джордж Пойа, Математическое открытие. Решение задач: основные понятия, изучение и преподавание, М.: Наука, 1976, 448 с.










