В данной статье мы рассмотрим само понятие золотого сечения, связь с природой и искусством, а также ответим на интересный вопрос касательно связи золотого сечения с великими пирамидами.
Ключевые слова: золотое сечение, пропорция, соотношение.
Прежде всего, стоит изучить понятие пропорции, формулировка которого звучит следующим образом: «Пропорция (от латинского proportio)– это равенство между двумя отношениями четырёх величин: a:b=c:d».
В качестве примера мы рассмотрим некоторый отрезок AB, на котором будет отмечена точка C, являющейся серединой отрезка. ( Рис. 1 ). Тогда мы можем утверждать, что AB:AC=AB:BC. Здесь мы рассмотрели ситуацию, когда полученные отрезки будут равны между собой.
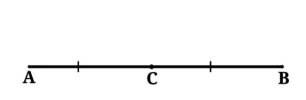
Рис. 1. AB:AC=AB:BC
Тот же отрезок AB мы можем разделить таким образом, что BC:AC=AC:AB ( рис. 2 ). Тогда мы можем утверждать, что отрезок разделен по золотому сечению или разделен в крайнем и среднем отношении.
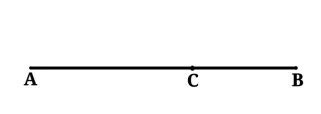
Рис. 2. BC:AC=AC:AB
Из вышесказанного следует, что золотое сечение — это такое пропорциональное гармоническое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей.
Первое чёткое определение соотношения (позже ставшее известным как золотое сечение) дал примерно в 300 году до н.э Евклид Александрийский, основатель геометрии как формальной дедуктивной системы.
Кто бы мог подумать, что такое, как может показаться с первого взгляда, невинное разделение отрезка, которое изначально определил Евклид в чисто геометрических целях, окажет влияние на самые разные области знаний– от ботаники до структур галактик, от математики до искусства? Можно сказать, что золотое сечение– прекрасный пример того самого восторга, который высоко оценён великим физиком Альбертом Эйнштейном. Он писал так: «Самое прекрасное, что только может выпасть нам на долю, — это тайна. Стремление разгадать её стоит у колыбели подлинного искусства и подлинной науки. Тот, кто не знает этого чувства, утратил любопытство, не способен больше удивляться, — все равно что мертвый, все равно что задутая свеча».
Точное значение золотого сечения (то есть, АС:СВ на рис. 2)– бесконечное непериодическое число 1,6180339887..., а такие бесконечные неповторяющиеся интересовали людей еще со времён античности.
В профессиональной математической литературе золотое сечение было принято обозначать греческой буквой τ (тау)– от греческого слова Τομή, что в переводе означает «сечение» или «развез». Но в начале 20го века американский математик Марк Барр предложил изменить обозначение золотого сечения с «τ» на «φ». Такое обозначение было выбрано не просто так, а по первой букве имени великого древнегреческого скульптора Фидия, жившего в ≈490–430 гг. до н. э. Величайшие шедевры Фидия, которые вероятно вам уже знакомы — Афина Партенос в Афинах и Зевс в Олимпии. Барр решил почтить память скульптора, поскольку многие искусствоведы полагают, что Фидий часто применял золотое сечение в своих творениях.
Золотой прямоугольник
Далее речь пойдёт о так называемом «золотом прямоугольнике. Длины его сторон соотносятся друг с другом в соответствии с золотым сечением, за что и получил данный прямоугольник звание «золотого» (A+B:A= φ). Теперь предположим, что мы отрежем от этого прямоугольника квадрат, как показано на рисунке ( рис. 3 ). У нас получится еще золотой прямоугольник (A:B= φ), только уже с меньшим размером, в сравнении с прошлым. Габариты этого «производного» прямоугольника меньше, чем у «исходного», с коэффициентом равным φ.
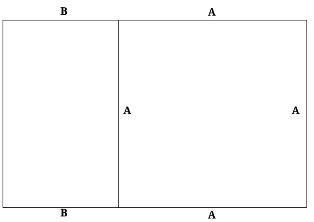
Рис. 3
Теперь снова отсечём квадрат, но уже от «производного» прямоугольника. Мы снова получим золотой прямоугольник, габариты которого опять же меньше с коэффициентом φ. Этот процесс можно продолжать бесконечно, получая золотые прямоугольники всё меньше и меньше.
Золотой прямоугольник — единственный прямоугольник, обладающий таким свойством, что если отрезать от него квадрат, получится подобный прямоугольник.
Если провести диагонали в любой паре из «исходного» и «производного» прямоугольников, как показано на рисунке ( рис. 4 ), то они пересекутся в одной точке.
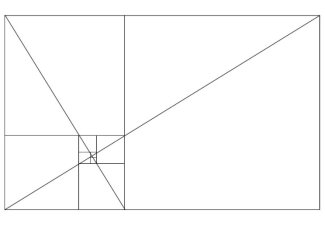
Рис. 4
К этой недостижимой точке, получившая пышное название «Око Господне», и сходятся уменьшающиеся прямоугольники.
Золотой треугольник
Золотой треугольник чем-то похож на золотой прямоугольник, рассмотренный нами ранее.
Золотым треугольником является такой равнобедренный треугольник, в котором сторона относится к основанию в золотом сечении.
Если изначально брать один золотой треугольник, а после биссектрисой разделить один из углов основания–мы получим тоже золотой треугольник, но уже поменьше. Ситуация действительна подобна отделению квадратов в золотом прямоугольнике. Как не сложно понять, при последующем делении треугольников на такие же, но с меньшим размером–получим «водоворот» из треугольников. ( Рис. 5 )
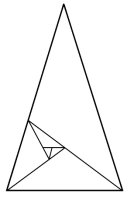
Рис. 5. Золотой треугольник
Числа Фибоначчи
Леонардо Пизанский (известный также как Леонардо Фибоначчи)– итальянский математик, начал свою первую и самую известную книгу– «Liber abaci», вышедшую в свет в 1202 году. Именно там он предложил свою последовательность в виде задачи с кроликами. Задача звучит таким образом:
«Некий человек поместил пару кроликов в огорожденное со всех сторон место. Сколько пар кроликов произойдет от этой пары за год, если предположить, что каждый год каждая пара порождает новую пару, которая еще через месяц становится способна приносить потомство?"
На рисунке ниже ( рис. 6) пара взрослых кроликов обозначена более крупной фигурой, а пара молодых — мелкой. Когда проходит первый месяц, первая пара порождает еще пару, их становится уже две. Когда проходит второй месяц, взрослая пара порождает еще одну молодую пару, а молодая пара тем временем подрастает. Теперь у нас уже три пары. Когда проходит третий месяц, каждая из взрослых пар порождает еще по паре, а молодая пара подрастает. Таким образом, у нас уже пять пар. Под конец четвёртого месяца, точно таким же образом, мы получим уже восемь пар. А на пятый месяц, соответственно, уже тринадцать пар.
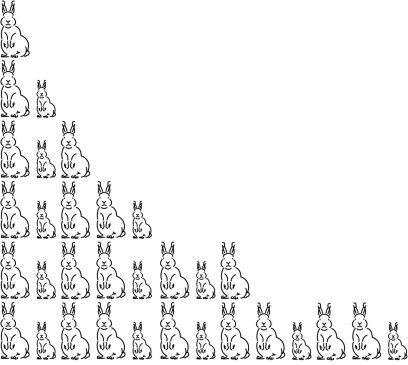
Рис. 6. Зависимость количества пар от месяца
Выявив закономерность, мы можем составлять последовательности чисел. Предположим, что нам интересны только взрослые пары в каждый определённый месяц. Это число будет состоять из числа взрослых пар в прошлом месяце + количество молодых пар (успевших к данному моменту повзрослеть) в тот же прошлый месяц. Однако мы можем пометить, что количество молодых пар месяц назад будет в точности равно количеству взрослых пар в позапрошлом месяце. Тогда в каждый конкретный месяц начиная с третьего, количество взрослых пар будет равно сумме количества взрослых пар в предыдущие два месяца. Тогда рассматривая количества взрослых пар, мы получаем последовательность: 1, 1, 2, 3, 5, 8, 13...
Из рисунка мы также понимаем, что количество юных пар будет подчиняться той же последовательности, но со сдвигом на месяц: 0, 1, 1, 2, 3, 5, 8, 13...
А значит общее количество пар — сумма последовательностей, которая совпадает со значением чисел последовательности для количества взрослых пар без числа за первый месяц.
Последовательность, в которой каждое число, начиная с третьего, равняется сумме двух предыдущих чисел, получило название «Числа Фибоначчи».
Числа Фибоначчи являются первой известной рекурсивной последовательностью (Рекурсивной называют ту последовательность, в которой отношение между соседними членами выражаются математической формулой). Математически это выражается следующим образом:
F(n+2)=F(n+1)+Fn. Где n– номер члена последовательности, F(n+1)–следующий член последовательности, а F(n+2)– член последовательности, следующий за F(n+1).
Также, числа Фибоначчи можно назвать золотыми.
Вернёмся к последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
Рассматривая отношения членов последовательности, мы сможем заметить, что чем дальше мы продвигаемся по последовательности Фибоначчи, тем ближе отношение двух соседних чисел будет к значению золотого сечения (колебаться около него). Например:
89/55 ≈1,6180561
144/89 ≈1,617977
233/144 ≈ 1,618056
610/377 ≈ 1,618037 и т.д
Логарифмическая спираль
Логарифмическая спираль и золотое сечение не отделимы друг от друга. Также можно подметить, что природа обожает логарифмические спирали. Одна только раковина моллюсков чего стоит, но это не единственный пример, когда спираль можно увидеть в природе. Приглядитесь к паутине, урагану, молекуле ДНК, которая также закручена в спираль.
Как же такую спираль можно построить?
Вспомним про золотые прямоугольники. Рассматривались сложенные воедино прямоугольники, полученные нами при делении одного «исходного» прямоугольника на квадрат и прямоугольник меньше. Если последовательно соединить точки, в которых квадраты делят стороны в золотом сечении, то мы получим логарифмическую спираль, сворачивающуюся к той самой точке, где пересекались когда-то диагонали. ( Рис. 7 )
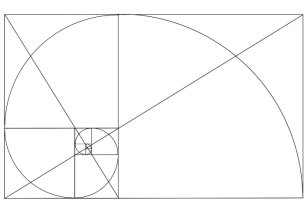
Рис. 7. Построение логарифмической спирали № 1
Помимо такого варианта, также есть возможность получить спираль из золотого треугольника, который уже рассматривался ранее. При соединении вершин золотых треугольников, то мы также получим логарифмическую спираль ( Рис.8 ).
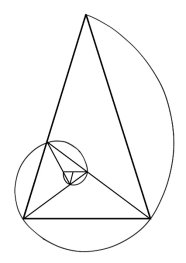
Рис. 8. Построение логарифмической спирали № 2
Связана ли великая пирамида с золотым сечением?
Вероятно, вы могли подумать, что одно из чудес света — пирамида Хеопса, которое словно окутано мистикой, было возведено, опираясь на золотое сечение. Сейчас мы постараемся ответ на вопрос, касаемо реальности данного заявления.
Писатель и популяризатор науки Мартин Гарднер в своей книге «Чудачества и заблуждения во имя науки» упоминает утверждение, которое, если является истинным, доказывает, что золотое сечение действительно использовалось при проектировании великой пирамиды. Он пишет: «Геродот утверждает, что пирамиду построили с таким расчетом, чтобы площадь каждой грани равнялась площади квадрата, сторона которого равна высоте пирамиды». Геродота, греческого историка, великий римский оратор Цицерон назвал «отцом истории». Гарднер не понимал, что следует из утверждения Геродота, однако он был не первым и не последним, кто затрагивает это утверждение.
Сравнительно недавно, в 1999 году, французский писатель и специалист в области телекоммуникаций Мидхаг Газале написал в своей книге «Гномон. От фараонов до фракталов»: «Говорили, что греческий историк Геродот узнал у египетских жрецов, что квадрат высоты великой пирамиды равен площади ее треугольной боковой стороны». Это утверждение так важно, потому что это равно высказыванию о том, что великая пирамида Хеопса была создана так, что отношение высоты ее треугольной стороны к половине стороны основания равно золотому сечению.
Рассмотрим чертеж пирамиды (рис. 9)
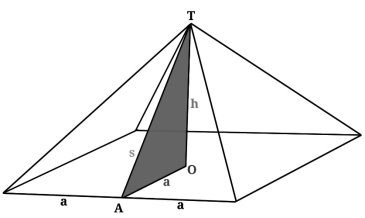
Рис. 9. Чертёж пирамиды
Если утверждение, приписанное Геродоту, верно, тогда это будет значить, что h²= s×a (квадрат высоты пирамиды равен площади треугольной стороны). Элементарные геометрические выкладки показывают, что это равенство значит, что соотношение s/a будет в точности равно золотому сечению, действительно ли это так?
На самом деле, основание великой пирамиды не совсем идеальный квадрат, длины сторон разнятся от 755,43 до 756,08 футов. Средняя длина стороны (2а) равна 755,79 футов. Высота пирамиды h=481,4 фута. Применив теорему Пифагора (h²+a²=s²), мы получим, что высота треугольной стороны s равна ≈612 футов. Тогда отношение s/a≈612/377,895≈1,619, что действительно, очень близко к золотому сечению.
Тогда получается, что древние египтяне действительно знали, что такое золотое сечение, поскольку φ встречается не просто в параметрах пирамиды, но и существует исторический документ, подтверждающий, что именно таким было намерение создателей сооружения: нам об этом говорит Геродот.
Очевидно, что параметры пирамиды неизменяемые, поэтому единственная «доказательная часть» наличия золотого сечения, в которой можно усомниться, состоит из утверждения Геродота.
Однако мы можем ознакомиться с классическим переводом оригинального отрывка (содержится в 124 параграфе книги II «Истории» Геродота): «Она четырёхсторонняя, каждая сторона её ширины в 8 плефров и такой же высоты». Стоит подметить, что плефр ≈ 100 греческих футов (примерно 101 английских).
Также заметим, что этот текст не совсем схож с тем, что нам представили как цитату Геродота (что квадрат высоты равен площади стороны). Более того, параметры пирамиды, приведённые самим Геродотом, вообще не соответствуют действительности. Великая пирамида высотой 481 футов, а не 800, и её сторона квадратного основания (≈756 футов) тоже существенно меньше 800 футов.
Откуда же тогда взята эта «цитата»?
Джон Тайлор, автор книги «Великая пирамида. Кто и зачем её построил?», начинает писать с перевода Геродота, не слишком отличающийся от процитированного: «Каждая грань этой пирамиды, которых четыре, с каждой стороны имеет по восемь плефров, и высота такова же». Однако тут автор дает волю воображению– и предполагает, что Геродот имел в виду, будто количество квадратных футов в квадрате со стороной, такой же, как высота пирамиды. Однако остаётся одна трудность– упомянутое число (8 плефров) сильно отличается от действительных размеров. Однако Тейлор предлагает способ преодоления данной трудности, который еще более возмутительный.
Без какой-либо логической аргументации он заявляет, что требуется умножить 8 плефров на площадь основания одной из меньших пирамид, стоящих к востоку от пирамиды Хеопса.
Из этого следует, что текст Геродота едва ли можно считать документальным подтверждением наличия золотого сечения в проекте великой пирамиды.
Также стоит сказать и о том, что некоторые египтологи утверждают, о наличии свидетельств, утверждающих о том, что при проектировании великих пирамид не учитывалось золотое сечение. Теория основана на принципе секеда. Секед — мера наклона граней пирамиды, а точнее, количество горизонтальных локтей, на которое надо было сместиться на каждый вертикальный локоть. С данной теорией согласны не все, но Роджер Герц-Фишер, изучивший 9 теорий, претендующих на истолкования проекта великой пирамиды, в статье, опубликованной в журнале «Crux Mathematicorum», пришёл к выводу, что теория секеда, весьма вероятно, верна.
Тогда мы можем быть уверены, что крайне маловероятно, чтобы золотое сечение было задействовано в построении великих пирамид.
Золотое сечение в искусстве
Очень кстати выше были рассмотрены великие пирамиды, которые также могут быть связаны с искусством, которое мы будем рассматривать далее.
В искусстве выделяют два основных направления: реализм и идеализм. Согласно с реалистическим взглядом, установление определённых норм для соотношения человеческого тела является излишним, так как задачей художника всегда является изображение данного частного тела, а не изменения, с целью «подогнать» под правильные пропорции. В случае с направлением–идеализмом, дела обстоят иначе. Идеалист, видит в человеке, как предмете изображения, родовое понятие, а не отдельного человека. Художник стремится передать определённый тип, а не отдельную модель. Стоит подметить, что если нахождение «нормального типа» человеческого тела, и будет иметь научное обоснование, то всё же будет присутствовать зависимость от пола и возраста. Всё это не позволяет нам надеяться на то, что в человеческом теле может присутствовать точные соотношения размеров, подобных отношению золотого сечения.
Самый простой вид осуществления золотого сечения в человеческом теле заключается в том что всё тело должно поясом делиться в отношении золотого сечения. Также известное правило: лоб, нос и нижняя часть лица должны быть равны, а дополняется тем, что рот делит нижнюю часть лица в отношении золотого сечения, точно также как и брови делят всю голову в том же самом отношении. Но достаточно очевидно, что такие грубые правила не претендуют на то, чтобы быть строго выполненными. Имеют только то значение, что делает созданное с их учётом изображение производит естественное и правильное впечатление. То есть получается, что подобные пропорции созданы для достижения одного результата–благоприятного восприятия.
Вероятно, вы могли подметить, что большинство картин выдающихся художников построены таким образом, что главный объект сдвинут с середины холста вправо или влево и находится на линии золотого сечения прямоугольника картины. Такой сдвиг смыслового центра с геометрической середины обусловлен особенностью зрительного восприятия. А сама особенность, в свою очередь, связана со зрительными путями мозга. Когда мы рассматриваем что-то в натуре, глаз фиксирует главное, всегда отдавая предпочтение правой или левой части поля ясного зрения. Перед наглядным примером смещения и применения золотого сечения в картине, следует практически ознакомиться с золотым сечением геометрическим способом. ( Рис. 10 ). Первоначально мы имеем отрезок АВ. Из точки B был проведён перпендикуляр, равняющийся половине AB. Полученной точке присвоим букву C. Эта самая точка C соединяется линией с точкой А. На полученной линии откладывается отрезок BC, который заканчивается новой точкой– D. Отрезок AD переносится на прямую АB. Полученная нами точка Е делит отрезок АВ в соотношении золотой пропорции. АЕ= 0,618..., если принять АВ за единицу, ВЕ=0,382... На практике используется округленные значения: 0,62 и 0,38. Тогда если отрезок АВ считать за 100 частей, то часть отрезка будет равна 62, а меньшая, соответственно, — 38 частям.
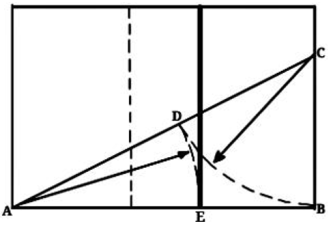
Рис. 10
Наконец, мы можем рассмотреть картину, в построении которой было задействовано золотое сечение. Фигура Пушкина в картине «А. С. Пушкин в акте в лицее 8 января 1815 года» И. Е. Репина помещена на линии золотого сечения в правой части холста. Левая часть, в свою очередь, также разделена в пропорции золотого сечения: от головы А. С. Пушкина до головы Г. Р. Державина и от неё до левого края картины. Также расстояние от головы Державина до правого края картины разделено на две равные части. В нижней части картины также можно уловить деление на три равные части. Их образуют стол в левой части, нога Пушкина правее линии золотого сечения и правый край картины. ( Рис. 11 )
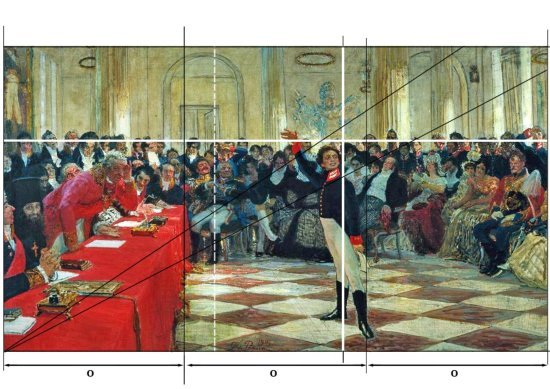
Рис. 11. Применение золотого сечения в картине И.Е Репина «А. С. Пушкин на акте в лицее 8 января 1815 года»
Конечно, множество картин построено с учётом золотых пропорций, но мы рассмотрели только один случай, поскольку как уже сказано, подобных картин очень много, отчего рассмотреть каждую является задачей не из лёгких.
Золотое сечение в природе
Ранее было сказано про человеческое тело и «нормальность» пропорции, теперь стоит рассмотреть явления золотых пропорций в прочих объектах, также сотворённых природой.
Вспомните подсолнух. Если внимательно посмотреть, то можно заметить, что его семена образуют спиральные узоры, также важно, что закручены в две стороны (по часовой стрелке и против неё соответственно). Очевидно, что семечки растут так, чтобы горизонтальное пространство между ними было оптимально. Количество спиралей зависит, чаще всего, от размера самого цветка. Как правило, их 34 в одну сторону и 55 в другую, но ученым также попадались и подсолнухи с соотношением количества спиралей 89/55, 144/89. Ранее уже были рассмотрены числа Фибоначчи и, как мы можем верно подметить, соотношения количества спиралей в точности соотношение соседних двух чисел из последовательности Фибоначчи. Двигаясь дальше по цветам, нельзя не подметить ромашку и розу. Что касается первого растения, то у большинства полевых ромашек 13, 21 или 34 лепестков– и это тоже числа Фибоначчи! Было бы чудесно заранее знать, четное или нечетное количество лепестков при гадании «любит–не любит». Расположение лепестков розы– прелестного, нежного цветка, символизирующего нежные чувства, также основано на золотом сечении. Если снимать с розы по лепестку, то станет видно, что её тесно прижатые друг к другу лепестки крепятся определённым образом. Предлагается рассмотреть схему ( рис. 12 ), на которой лепестки пронумерованы.
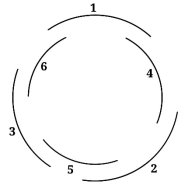
Рис. 12. Схема расположения лепестков розы
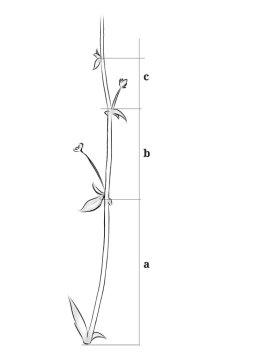
Углы, определяющие положение лепестков– это дробные части произведений φ на целые числа. Таким образом, лепесток № 2 расположен в 0,618 оборота от лепестка № 1 (дробная часть от произведения: 1×φ), лепесток № 3 в 0,236 оборота от лепестка № 2 (дробная часть от 2×φ) и так далее. Не отходя от цветов, также стоит вспомнить и про цикорий — непримечательное, придорожное растение. Приглядимся к нему более внимательно ( рис. 13 ). От основного стебля образовался отросток, там же образовался и первый листок. (На данном этапе необходимо вспомнить про те числа, которые брались нами при рассмотрении искусства). Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс мы возьмём за 100 некоторых единиц, то второй равен 62 единицам, третий–38, четвёртый–24 и т. д. Длина лепестков также подчинена золотой пропорции. Импульсы роста растения постепенно уменьшались в пропорции золотого сечения. Отойдя от растений, рассмотрим представителя животного мира, в чьем теле сразу можно уловить приятные для нашего взора пропорции ( рис. 14 ).
|
|
|
|
Рис. 13. Стебель цикория |
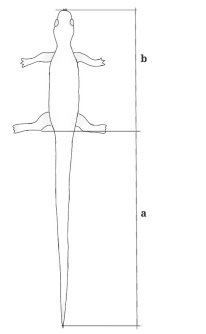
Рис. 14. Тело ящерицы |
Мы рассматриваем ящерицу. Длина её хвоста относится к длине остального тела, как 62 к 38 (значения будут приблизительно равны. Например: a=19, b=11,6. а/b≈62/38).
Мы можем рассматривать бесконечное множество памятников культуры, творений природы и даже тех объектов, которые бесцельно находятся у нас под рукой– вероятно во многих, будут замечены следы золотого сечения. Золотое число φ или, заслуженное звание «Божественной пропорции», встретившиеся нам в пропорциях чудесного–указывает на связь математики и её значимость в прочих сферах, доказывая её величие и могущество.
Литература:
- «φ– Число Бога. Золотое сечение–формула мироздания». Марио Ливио
- «Золотое сечение в живописи». Ф. В. Ковалев
- «Золотое сечение». Г. Э. Тимердинг.