В статье автор исследует метод «Монте-Карло» и создаёт компьютерную модель этого метода.
Ключевые слова: метод, Монте-Карло, вероятность, статистика, статистические методы, компьютерная модель.
Метод Монте-Карло представляет собой мощный инструмент для анализа случайных процессов и решения задач, связанных с вероятностью. Разработка Метода стала значительным шагом вперед в области математического моделирования, и с тех пор он нашел широкое применение в различных областях, включая физику, финансы, инженерию и другие.
Одним из ключевых преимуществ метода Монте-Карло является его способность эффективно обрабатывать сложные системы, где традиционные аналитические методы могут оказаться неэффективными или невозможными. Например, в ситуациях с многомерными распределениями или сложными зависимостями между переменными метод Монте-Карло может предоставить более точные результаты за счет использования случайных выборок и статистических методов.
Конечно, ни один метод не может гарантировать абсолютную точность, однако метод Монте-Карло часто превосходит традиционные подходы по скорости и точности вычислений в условиях неоднозначности. Это делает его особенно ценным в реальных приложениях, где необходимо учитывать случайные колебания и неопределенности.
Таким образом, метод Монте-Карло не только расширяет возможности математического моделирования, но и предоставляет более реалистичное представление о сложных системах, что делает его важным инструментом для исследователей и практиков в различных областях.
Джон фон Нейман и Станислав Улам изобрели моделирование методом Монте-Карло в 40-х годах прошлого столетия. Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом, а одним из простых механических приборов для получения случайных величин является рулетка.
Работает метод следующим образом. Вместо того чтобы строить сложную математическую модель, мы берём исходное уравнение, описывающий исследуемый процесс, и подставляем в него случайные числа. Проводим вычисления в зависимости от переменной (или нескольких переменных) и получаем результат с нужной нам точностью. Чем больше берём случайных чисел — тем точнее получается результат.
Рассмотрим в качестве примера подбрасывание монеты. Эта задача содержит неопределенность: так как мы не можем быть точно уверенны в том, что выпадет «орел» или «решка». Пусть требуется найти некоторую величину (например, долю выпадения «орлов»). На ЭВМ с помощью генератора случайных чисел имитируются ситуации или процессы, возможные по условию задачи и приводящие к тем или иным исходам.
При этом искомая величина принимает некоторые значения. Все или почти все исходы (с учетом, когда монета может упасть на ребро) проявятся, если многократно рассмотреть случайное развитие одного и того же начального состояния (смоделировать некоторое количество историй).
Изначально, этот метод применялся для решения задач нейтронной физики, где численные методы, как стало известно, менее информативны. Его действие стало хорошо известным на широком круге задач статистической физики, очень различных по своему содержанию. К разделам науки, где всё в большей степени применялся метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других. На методах Монте-Карло основано много полезного: моделирование облучения твёрдых тел ионами в физике, моделирование поведения разреженных газов, исследования поведения разных тел при столкновении, алгоритмы оптимизации и нахождения кратчайшего пути решения (задача коммивояжера), решение сложных интегралов (или когда их очень много), предсказание астрономических наблюдений, поиск в дереве в различных алгоритмах, алгоритмы работы некоторых функций квантового компьютера, моделирование состояния приближённой физической среды.
Компьютерная программа реализована на языке Python. Слоты рулетки, обозначены переменной slots. Всего использовано 37 слотов: от 0 до 36 включительно. Соответственно, броски шарика («испытания»), обозначены переменной tries. Далее идёт команда, которая показывает, какие различные, случайно выбранные числа могут выпасть при 100 бросаний мячика. Работа этой программы позволяет убедиться в том, что получаемое распределение абсолютно хаотично.
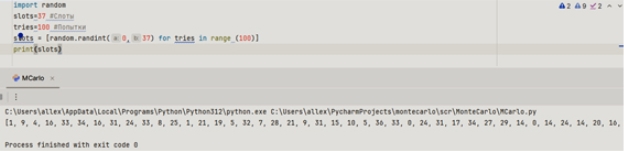
Рис. 1. Фрагмент программы для исследования распределения случайной величины
В то же время, если построить гистограмму выпавших чисел при ста попытках, то распределение получается неравномерным.
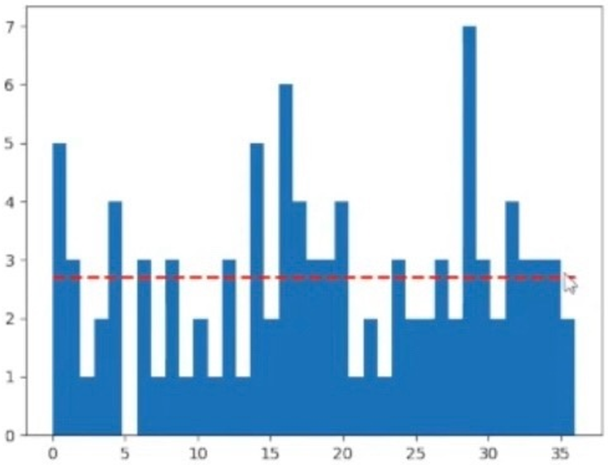
Рис. 2. Гистограмма распределения случайной величины при 100 измерениях
Чтобы «исправить» это несовпадение необходимо увеличить количество попыток, допустим, в 100 раз. Получается, что на 10000 попыток программа будет выдавать в среднем числа, шанс выпадения которых будет максимально приближен к математической модели. Как мы можем увидеть, результат приблизился к действительности.
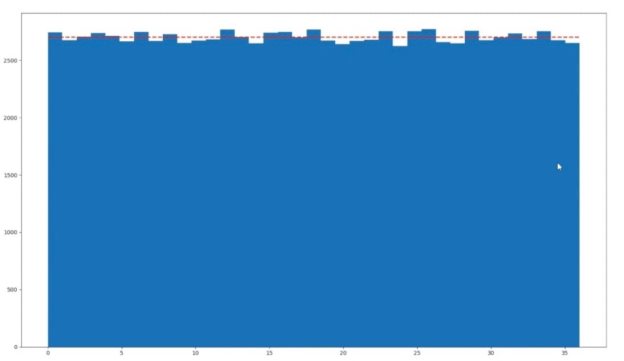
Рис. 3. Гистограмма распределения случайной величины при 10000 измерениях
Результат математической модели сохраняется в переменной average, которая вычисляется делением слотов на количество бросков.
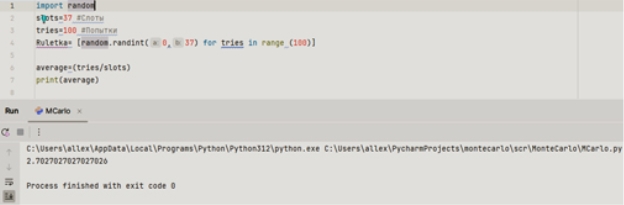
Рис. 4. Вычисление частоты выпадения того или иного числа
Далее, создаем словарь bookOfResult, который поможет впоследствии обратиться к случайно выпавшим числам. В словаре ищем частоту выпадения того или иного числа на всех рассмотренных подбрасываниях, это условие мы записываем в переменную probilityOfAnyResult, то есть ожидаемое выпадение любого числа от 0 до 36. Допустим, какова вероятность выпадения числа 26. Вычисление вероятности выпадения любого, конкретно выбранного числа — это отношение одного к количеству слотов, это условие мы записываем в переменную mathematicallyExpected. И в завершении осуществляется вывод вероятности выпадения числа по теории метода Монте-Карло, сравнивая его, с выведенной стандартной теорией вероятности. Как мы можем увидеть расхождение в ответах минимальное, но не стоит забывать, что метод Монте-Карло изначально учитывает неопределенность, и мы считаем, что это делает его более точным.
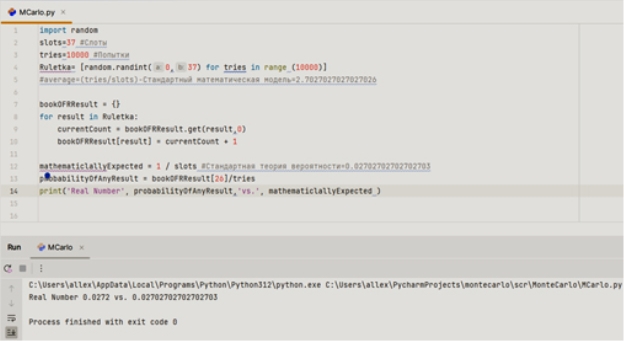
Рис. 5. Программа, реализующая метод Монте-Карло
В итоге настоящей работы, посвященной проверке метода по таким критериям, как: достоверность, эффективность, точность, область применения и другие, можно сделать вывод о том, что метод Монте-Карло не только действительно работает, но и опережает стандартные математические методы решения задач на вероятность.
В работе раскрыта суть метода Монте-Карло и создана компьютерная модель данного метода. Как можно увидеть, результат, получаемый благодаря данному подходу, не совершенно близок к идеалу, но, как говорил Дипак Чопра «Неопределенность есть данность, потому что жизнь не что иное как изменение». И именно из-за этой неопределенности данный метод более точный, как бы ни парадоксально это было.










