В мире развития информационных технологий, и увеличения количества данных, обрабатываемых и передаваемых в цифровой форме, актуальным стал вопрос о защите информации и персональных данных. Человек совершая покупки в интернете, бронируя билеты, оформляя запись на прием к врачу, передает свои персональные данные третьим лицам. Можно ли быть уверенным, что они не попадут к злоумышленникам? Необходима защита переданной информации. Существует много способов хеширования информации. Автором статьи создан и протестирован алгоритм хеширования данных на основе функции Капрекара.
Ключевые слова: функция Капрекара, постоянная Капрекара, хеширование, криптография.
Актуальность темы обусловлена несовершенством существующих методов хеширования и повышенным спросом на данные алгоритмы защиты информации. В современном мире есть необходимость разработать несложный в применении алгоритм для защиты информации, устойчивый к взлому. Автором статьи разработан алгоритм хеширования на основе функции Капрекара и его реализация его на языке Python. Даттатрея Рамчандра Капрекар (1905–1986) получил среднее образование в Тейне, учился в Коттон-колледже в Гувахати, закончил Университет Мумбаи, получив степень бакалавра в 1929 году. С 1930г по 1962г он был школьным учителем в государственной начальной школе в Девлали Махараштре. Опубликовал работы на такие темы, как повторяющиеся десятичные дроби, магические квадраты, целые числа со специальными свойствами и стал хорошо известен в кругах любителей математики. Первоначально его идеи не были восприняты всерьез, работы опубликовали в математических журналах низкого уровня. Международная известность пришла, когда американский математик, писатель и популяризатор науки Мартин Гарднер написал о Капрекаре в своей колонке в марте 1975 г. в журнале Mathematical Games for Scientific. Сегодня многие математики продолжают изучение его открытий. Рассмотрим подробнее некоторые открытия Капрекара.
- Постоянная Капрекара, «неподвижные точки». Для любого четырёхзначного числа n, большего 1000, в котором не все цифры одинаковы можно проделать следующие операции. Расположить цифры сначала в порядке возрастания, затем в порядке убывания. Вычесть из большего меньшее (производя перестановки цифр и вычитания, нули следует сохранят). Повторяя этот процесс с полученным результатом, не более чем за семь шагов можно получить число 6174, которое будет затем воспроизводить само себя. Само число 6174 получило название постоянной Капрекара, а описанный выше алгоритм стали называть функцией Капрекара K(n). Рассмотрим пример. Возьмем число n = 1234:
– n = 1234: min = 1234, max = 4321 => 4321 − 1234 = 3087;
– n 1 = 3087: min = 0378, max = 8730 => 8730 − 0378 = 8352;
– n 2 = 8352: min = 2358, max = 8532 => 8532 − 2358 = 6174.
Если продолжить описанный алгоритм, то получим следующее:
– n = 6174: min = 1467, max = 7641 => 7641–1467 = 6174.
Дальнейшие итерации будут приводить к константе 6174.
Если рассмотреть натуральные числа с другим количеством разрядов, то функция Капрекара будет сходится к другим постоянным числам. Например, для трехзначных чисел такой константой станет число 495. Такие постоянные значения называют «неподвижными точками». Причем в некоторых случаях точка не определена, но есть некая зацикленная цепочка преобразований. Ниже дана таблица значений постоянной Капрекара для разного количества разрядов числа (число 0 — тривиальная постоянная Капрекара).
|
Количество разрядов в числе |
Значение постоянной Капрекара |
|
2 |
----------------- |
|
3 |
495 |
|
4 |
6174 |
|
5 |
----------------- |
|
6 |
631764, 549945 |
|
7 |
----------------- |
|
8 |
97508421, 63317664 |
|
9 |
864197532, 554999445 |
|
10 |
9753086421, 6333176664, 9975084201 |
|
11 |
86431976532 |
|
12 |
975330866421, 633331766664, 555499994445, 997530864201, 999750842001 |
|
13 |
8643319766532 |
|
14 |
97755108844221, 97533308666421, 63333317666664, 99753308664201, 99975308642001, 99997508420001 |
|
15 |
864333197666532, 555549999944445 |
|
16 |
9775531088644221, 6333333176666664, 9753333086666421, 9977551088442201, 9975333086664201, 9997533086642001, 9999753086420001, 9999975084200001 |
|
17 |
98765420987543211, 86433331976666532 |
|
18 |
886644219977553312, 977553310886644221, 975333330866666421, 633333331766666664, 555554999999444445, 997755310886442201, 997533330866664201, 999775510884422001, 999753330866642001, 999975330866420001, 999997530864200001, 999999750842000001 |
|
19 |
9876543209876543211, 8643333319766666532, 9987654209875432101 |
|
20 |
88664432199776553312, 97755333108866644221, 63333333317666666664, 97533333308666666421, 97775551108884442221, 99775533108866442201, 99753333308666664201, 99977553108864422001, 99975333308666642001, 99997755108844220001, 99997533308666420001, 99999753308664200001, 99999975308642000001, 99999997508420000001 |
Для пятизначных и семизначных чисел существует следующие цепочки:
– 74943 -> 62964 -> 71973 -> 83952 -> 74943 -> …
– 63954 -> 61974 -> 82962 -> 75933 -> 63954 -> …
– 53955 -> 59994 -> 53955 -> …
– 8429652 -> 7619733 -> 8439552 -> 7509843 -> 9529641 -> 8719722 -> 8649432 -> 7519743 -> 8429652 -> …
Подобные цепочки также существуют и в том случае, если постоянная Капрекара определена. Например, для девятизначных чисел:
– 865296432 -> 763197633 -> 844296552 -> 762098733 -> 964395531 -> 863098632 -> 965296431 -> 873197622 -> 865395432 -> 753098643 -> 954197541 -> 883098612 -> 976494321 -> 874197522 -> 865296432 -> …
- Числа Капрекара — целые положительные числа, обладающие свойством: если число возведено в квадрат, то его представление можно разделить на две целые положительные части, сумма которых равна исходному числу («операция Капрекара»). Например, 45 (45 2 = 2025, и 20 + 25 = 45), 9 (9 2 = 81, 8+1 = 9), 55 (55 2 = 3025, 30+25 = 55), 99 (99 2 = 9801, 98+01 = 99) и другие. Однако существует ограничение: эти два числа должны быть положительными. Поэтому, например, число 100 не является числом Капрекара, хотя 100 = 10000 и 100+00 = 100.
- Числа харшад («великой радости») — натуральные числа, делящиеся нацело на сумму своих цифр. Таким числом является, например, 1729, так как 1729 / (1 + 7 + 2 + 9) = 91. Очевидно, что все числа от 1 до 10 являются числами харшад. Подобным свойством обладают и некоторые из постоянных Капрекара. Так, число 6174 / (6 + 1 + 7 + 4) = 343.
- Числа Демло. Д. Р. Капрекар определил числа Демло так: «объединение левой, средней и правой частей, где левая и правая части должны быть одинаковой длины (вплоть до возможного начального нуля слева) и должны в сумме давать некоторое значение, которое может повторяться неоднократно». Дальнейшие изучения показали, что числа Демло представляют собой квадраты репьюнитов — натуральных чисел, которые в любой позиционной системе счисления записываются одними единицами. Самыми известными являются «чудесные числа Демло»: 1, 121, 12321, 1234321, ..., которые представляют собой квадраты репьюнитов 1, 11, 111, 1111,....
- Самопорожденные числа (числа Девлали) — числа, которые нельзя получить сложением какого-либо другого числа, называемого генератором, с суммой его цифр. Например, число 58. Его можно получить, если добавить к числу 47 сумму его цифр 11: 57 + (4 + 7) = 58. Таким образом, число 58 не является самопорожденным, т. к. для него существует генератор — число 47. А, например, число 20 нельзя получить из другого числа описанным выше способом. Поэтому оно является самопорожденным. Последовательность самопорожденных чисел: 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97, …
Рассмотренный выше алгоритм получения постоянных Капрекара для чисел в 10-ой системе счисления представляет собой итерационную функцию, обладающую интересными свойствами. Он может применяться для чисел в различных системах счисления. Основные свойства функции Капрекара:
- Все последовательности Капрекара либо достигнут одной из неподвижных точек, либо приведут к повторяющемуся циклу. В любом случае, конечный результат достигается за ограниченное число шагов.
- Наименьшее и наибольшее числа, составленные из исходного, имеют одинаковую сумму цифр и, следовательно, одинаковый остаток от деления
- на 9. Значит, каждое число в последовательности Капрекара кратно 9.
- Разность наибольшего и наименьшего чисел, составленные из исходного, делится на 10 2– 1 = 99.
- При составлении наименьшего и наибольшего числа из числа n, являющегося постоянной Капрекара, при нахождении разности этих чисел не изменяется состав цифр, а лишь их порядок в числе.
- Для чисел разрядностью 4 сумма крайних левой и правой цифры постоянных Капрекара равна 10.
- Сумма средних цифр постоянных Капрекара равна 8. Между крайними и средними цифрами могут находится разряды, сумма цифр которых равна 9.
- Сумма равноудаленных от краев цифр постоянных Капрекара равна 9.
- Среди всех постоянных Капрекара первая цифра меньше 5 только в случае трехзначных чисел (495); нет значений, начинающихся на цифру 7; если постоянная начинается на 5,6,7 или 8, то значение не содержит нулей.
- Исходя из свойства 2, само число n, либо значение, полученное после первой итерации функции Капрекара, делится на 9. То есть существует ограниченное множество натуральных чисел, к которым сходятся все другие числа сразу или после первого шага работы функции. Например, для 6174 имеем следующую схему перехода базовых четырёхзначных чисел, кратных 9, к соответствующему значению.
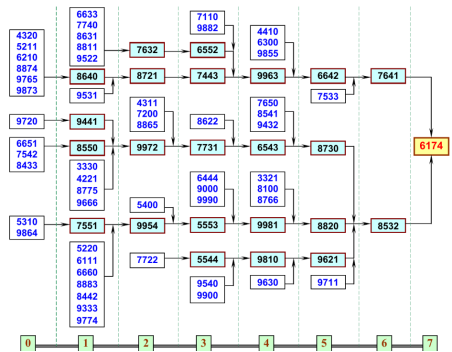
Тогда соответствующее множество четырехзначных чисел, кратных 9, к которым преобразуются другие числа, представим следующим образом:
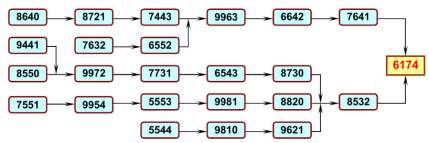
- Цифры четырехзначных чисел удовлетворяют соотношениям a ≥ b ≥ c ≥ d,
- a > 0, d < 9 и в процессе переходов подчиняются аналитическим формулам:
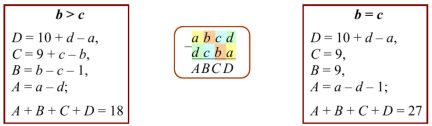
- Постоянная Капрекара 6174 обладает следующими свойствами:
– квадратный корень из суммы квадратов простых множителей числа — целое число:
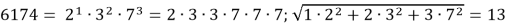
– число 6174 может быть представлено в виде:
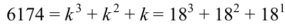
Алгоритм последовательного применения функции Капрекара является достаточно несложным, но в процессе вычислений происходит многократное преобразование чисел так, что исходное число изменяется кардинально и не подлежит восстановлению. Это свойство позволяет рассмотреть вопрос о применении алгоритма в качестве хеш-функции — функции, которая создает уникальный цифровой отпечаток из исходной информации. Хеш-функция осуществляет преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины по определённому алгоритму. Преобразование, производимое хеш-функцией, называется хешированием. Исходные данные называются входным массивом или «ключом», а результат преобразования — хешем или хеш-суммой.
Алгоритм хеширования работает только в одном направлении: из любого содержимого можно сгенерировать его хэш, но из хэша нельзя сгенерировать связанное с ним содержимое. На сегодняшний день существует множество алгоритмов хеширования, различающихся различными свойствами:
– разрядность — количество разрядов (битов) электронного устройства, одновременно обрабатываемых или передаваемых этим устройством;
– вычислительная сложность — функция зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных;
– криптостойкость — способность алгоритма противостоять криптоанализу.
В качестве хеш-функций часто выбирают математические преобразования. При этом «хорошая» хеш-функция должна удовлетворять двум свойствам:
– быстрое вычисление;
– минимальное количество «коллизий» — равенств значений хеш-функции на двух различных блоках данных. Т. е. это случай, при котором одна хеш-функция для разных входных блоков возвращает одинаковые хеш-коды.
Основные идеи работы алгоритма следующие: вкачестве основной математической функции для построения хеш-функции использовать алгоритм получения постоянных Капрекара, описанный ранее. Сам алгоритм получения хеша состоит из нескольких этапов:
- Ввод исходной строки.
- Получение ASCII-кодов каждого символа строки.
- Чтобы уменьшить вероятность получения коллизий, полученные значения кодов объединяются попарно.
- Расчет постоянных Капрекара по описанному алгоритму. Поскольку значение постоянной должно быть вычислено за 7 итераций цикла, то при превышении данного лимита шагов сохраняется текущее значение.
- Полученные постоянные Капрекара переводятся в 16-ричную систему счисления и объединяются в единую строку.
- Результат работы — 32 битное слово. Если количество символов в строке превышает 32, то происходит «свёртка». Строка разделяется по 4 символа, вычисляется модуль разности между десятичными значениями рядом стоящих элементов. Результат обратно переводится в 16-ричную систему и добавляется в новое значение хеша. Если после «свёртки» в исходной хеш-строке остались незадействованные элементы, то они добавляются в конец нового хеша. Этот процесс повторяется до тех пор, пока длина хеш-строки не станет меньше либо равна 32.
- Если количество цифр в результате меньше 32, то вперед добавляются незначащие нули.
Рассмотирм подробнее реализацию отдельных этапов алгоритма на Python.
Шаги 1–3. Перебор всех символов строки. Определение ASCII-кода и добавление в список, в котором хранятся непреобразованные числа. Затем происходит попарное объединение полученных кодов.


Шаг 4. Расчет значения постоянной Капрекара. Для каждого элемента из полученного списка строим список цифр, определяем наименьшее и наибольшее значения, которые могут быть получены из этих цифр и находим разницу между этими значениями. Данный процесс продолжается, пока не будет получена постоянна Капрекара или не будет выполнено 7 итераций цикла. Полученный результат добавляется в список констант.

Шаги 5–7. На данном этапе происходит сборка 16-ричных значений постоянных Капрекара в единую строку и контроль за размером полученной строки. Если количество символов отличается от 32, то используется либо цикл «свёртки» для уменьшения длины, либо дописываются незначащие нули.

Пример применения разработанного алгоритма. Составим таблицу хешей для наиболее популярных паролей в 2023 году. Российский сервис мониторинга утечек данных и даркнета Data Leakage & Breach Intelligence проводит ежегодное исследование, цель которого в определении самых популярных паролей среди интернет-пользователей. Источниками данных для анализа в компании служат различные сообщества, занимающиеся восстановлением паролей из хешей, теневые форумы и Telegram-каналы, где в открытый доступ выкладываются массовые утечки. Таблица хешей для топа паролей по данным сервиса DLBI:
|
Пароль |
Хеш |
|
123456 |
00000000000000000000181e181e181e |
|
123456789 |
000000000000000000181e181e181e00 |
|
qwerty123 |
000000000000cff1ecd494cff1e181e0 |
|
qwertyuiop |
00000000000cff1ecd494cff1e9a3d40 |
|
password |
0000000000001192566c0c9f564b74fb |
|
zxcvbnm |
0000000000000000d22a0f5f4f9d21ef |
|
guest |
000000000000000000066c0cb71771ef |
|
protected |
00000000000cd494b7177124bfb71770 |
|
1qaz@WSX |
0000000000000000f216f216181e181e |
|
1qaz!QAZ |
0000000000000000f216f216181e181e |
|
пароль |
0000000000052849e03c626a0515d80a |
|
привет |
0000000000052849e05173b1e3d58bfe |
|
люблю |
00000000000000515d80a4f5aa3a181e |
|
андрей |
00000000000000515d80a4f5aa3a181e |
|
максим |
0000000000052849e03d545ae5173b1e |
|
наташа |
0000000000047d1e63517816e5cfdc45 |
|
солнышко |
0000524f71853768ee52803904f5aa3a |
|
подружка |
00004f5aa3a4f5aa3a32db3493e65470 |
Видим, что в некоторых случаях полученный алгоритм приводит к коллизиям (к повторению хешей), так как для определенного диапазона чисел значение постоянной Капрекара может оказаться одним и тем же. Для этого необходимо неоднократное совпадение этих значений. Однако, поскольку алгоритм подразумевает последующую обработку полученных значений, количество коллизий не должны быть слишком высоким. Разработанный алгоритм был протестирован на большом количестве более длинных символьных выражениях — цитатах известных и великих людей. Примеры:
|
Высказывание |
Хеш |
|
Что разум человека может постигнуть и во что он может поверить, того он способен достичь |
00000000000029b81ce0b23175e7503e |
|
Сложнее всего начать действовать, все остальное зависит только от упорства |
00000000000000019bb2984b8cf42cac |
|
Логика может привести Вас от пункта А к пункту Б, а воображение — куда угодно |
00014072a37c4f74e63c882b663a97ee |
|
Начинать всегда стоит с того, что сеет сомнения |
0000000000001fc52eb57870b4ff1f2e |
|
80 % успеха — это появиться в нужном месте в нужное время |
0000000000033612233b147564b3404a |
|
Ваше время ограничено, не тратьте его, живя чужой жизнью |
000000009cd3b9921ab720dc1982a6e9 |
|
Вы никогда не пересечете океан, если не наберетесь мужества потерять берег из виду |
000000000000066bca657365d23c4b1e |
|
Два самых важных дня в твоей жизни: день, когда ты появился на свет, и день, когда понял, зачем |
000000000000034e444177de07db15ce |
|
Не волнуйтесь, если что-то не работает. Если бы всё работало, вас бы уволили. |
02f6eb16195114ce474a12f0d3809360 |
|
Измерять продуктивность программиста подсчетом строк кода — это так же, как оценивать постройку самолета по его весу. |
0000000008038e507ef186e3a047d880 |
|
Люди, которые думают, что ненавидят компьютеры, на самом деле ненавидят плохих программистов. |
00000000082341a12938fcc756de3800 |
|
Если вы дадите человеку программу, то займете его на один день. Если вы научите человека программировать, то займете его на всю жизнь. |
00000002952154f40a783fe8730c4c0c |
|
Язык, который не меняет вашего представления о программировании, недостоин изучения. |
000000000000079b1731b1a6064873d4 |
|
Неработающая программа обычно приносит меньше вреда, чем работающая плохо. |
2f30caf23fafb31f31df2a652444ff1e |
Понимаем, что для объемных фраз, а не для одного слова, хеши не повторяются, поскольку при построении первой версии хеш-строки получается довольно большая длина, при этом вероятность повторения комбинации кодов символов довольно низкая. А дальнейшая «свёртка» еще больше уменьшает появление коллизий.
Тестирование результатов работы программы показало, что алгоритм не является совершенных и в некоторых ситуациях может приводить к коллизиям. Однако даже у общепринятых методов хеширования существует подобная проблема. При тестировании такая проблема произошла в 2 из 40 запусков и только в случае с кодированием небольших слов, где велика вероятность повторения постоянных Капрекара в результате обработки символьной последовательности.
Таким образом, изучение свойств функции Капрекара, а также принципов работы хеш-функций позволило создать несложный алгоритм для защиты информации от взлома. При этом данный алгоритм может быть доработан с целью минимизации коллизий. Например, с помощью автоматизации процесса построения таблицы хешей с анализом и корректировкой получаемых результатов или с помощью метода повторного хеширования на основании другого алгоритма.
Литература:
- Василенко, С. Л. Инверсно-числовые аттракторы. URL: https://www.trinitas.ru/rus/doc/0016/001c/1686-vs.pdf (дата обращения: 12.01.2024).
- Галуев, Г. А. Математические основы криптологии: Учебно-методическое пособие / Г. А. Галуев — Таганрог: Изд-во ТРТУ, 2003. — 120с.
- Портал «Wikipedia». Статья «Хеш-функция» — URL: https://ru.wikipedia.org/wiki/Хеш-функция (дата обращения: 20.11.2023).
- Портал «Хабр». Статья «Феномен постоянной Капрекара» — URL: https://habr.com/ru/companies/bercut/articles/767488/ (дата обращения: 18.10.2023).
- Портал «Wikipedia». Статья «D. R. Kaprekar» — URL: https://en.wikipedia.org/wiki/D._R._Kaprekar (дата обращения: 22.10.2023).
- Портал «kaprekar.sourceforge» — URL: https://kaprekar.sourceforge.net/ (дата обращения: 15.12.2023).
- Портал «Tproger». Статья «100 самых актуальных цитат о программировании» — URL: https://tproger.ru/articles/programming-quotes?ysclid=lt1843suux886318755 (дата обращения: 02.02.2024).










