The article contains an independent study of the Collatz hypothesis and an analysis of some sources that have studied this problem.
Keywords: Collatz conjecture, the number module.
Introduction
Collatz conjecture, also known as 3n+1, is an unsolved problem, which was proposed in 1934 by German mathematics Lothar Collatz. The essence for the conjecture is that for any natural number n, the sequence is generated by the following rules: If number n is even, divide it by 2, if number n is odd, multiple it by 3 and add 1, will lead to 1. [1]
My experience
My initial thoughts were to analyze this through modular arithmetic. Assume that a counterexample exists — some number n. Then all numbers leading to n eventually converge to the number 1. Therefore, n must satisfy one of the following conditions: either n ≡ 0 (mod 4), or n ≡ 1 (mod 4), or n ≡ 2 (mod 4), or n ≡ 3 (mod 4). Let us consider all cases.
Let us represent the number n in the form n=4a, where a is natural integer. n=4a is even, so by dividing it by 2, we obtain 2a. 2a 4a=n, when n is natural. Thus, according to our assumption, we can derive the number 1 from all integers less than 4a. In particular, we can obtain 1 from 2a. Furthermore, since 4a can be expressed as 2 ×2a. It follows that if we can reduce 2a to 1, we can also reduce 4a to 2a.
Let us represent the number n in the form n = 4a + 1, which is odd. Consequently, the next operation will involve multiplying it by 3 and adding 1:
3 (4a+ 1) + 1 = 12a + 4.
This result is even. According to the rules of the Collatz conjecture, when we encounter an even number, our next step is to divide it by 2:
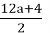
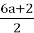
At this point, we need to analyze the relationship between our current result, 3a+1, and our original number, n = 4a + 1. Suppose that 4a + 1 < 3a + 1 possible. So, 4a < 3a. It means that 4a — 3a = a <3a − 3a = 0. We have confirmed that when a is natural, 4a + 1 > 3a + 1.
Thus, we conclude that after applying the Collatz operations starting from our initial assumption of the form n = 4a+ 1, we eventually arrive at a number that is smaller than our starting point. This indicates that this case does not satisfy our original assumption regarding the existence of a counterexample.
Now let us consider another scenario where the number n can be expressed in
the form n = 4a + 2, where a is a non-negative integer. This representation indicates that n is even, as it is two more than a multiple of 4. Since n is even, we apply the first operation of the Collatz conjecture, which involves dividing the number by 2:
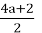
Now let’s compare 2a + 1 and 4a + 2.
4a + 2 = 2(2a + 1). So, when a is natural, 4a+ 2 obviously more than
2a + 1.
Thus, we conclude that after applying the Collatz operations starting from our initial assumption of the form n = 4a + 2, we eventually arrive at a number that is smaller than our starting point. This indicates that this case does not satisfy our original assumption regarding the existence of a counterexample. We now consider the scenario in which the number n can be expressed in the form n = 4a + 3, where a is a non-negative integer. To facilitate our analysis, we will examine the value of a on module 3.
Let’s consider the case, when a ≡ 2 (mod 3). Assuming that a ≡ 2 (mod 3), we can represent a as a = 3b + 2, where b is a non-negative integer. Substituting this expression into our original equation for n: n= 4a + 3 = 4(3b + 2) + 3 = 12b + 11.
Next, we must analyze how the number n = 12b + 11 could have been derived according to the rules of the Collatz conjecture. There are two primary possibilities:
- From some non-negative integer c, where 3c + 1 = 12b + 11
-
From some non-negative integer d, where
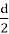
If we assume that n could have been derived from another number c, then we would have, that 3c + 1 = 12b + 11. This equation gives us that:
3c = 12b + 10 ⇒ c= 4b + 3
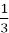
And since b must be an integer, the c= 4b + 3
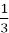
If n = 12b + 11 was obtained by dividing some even number d = 2 × (12b + 11) by 2, we can express this relationship as follows:
d = 2n = (12b + 11) × 2 = 24b + 22.
Now we need to examine how the number d = 24b + 22 could have been obtained through the Collatz operations. Let’s check, if we can get it by multiplying by 3 and adding 1. Then, some natural e satisfies the equality 3e + 1 = 24b + 22. Then, let’s pay attention on number 8b + 7. It’s odd, so our next step is multiplying it by three and adding one:
(8b + 7) × 3 + 1 = 24b + 22
It means, that 8b + 7 cannot be reduced to one. But according to our assumption, all numbers till 12b + 10 can — the contradiction.
Now let’s consider the case, when a ≡ 0 (mod 3). Assuming that a ≡ 0
(mod 3), we can represent a as a = 3b, where b is a non-negative integer. Substituting this expression into our original equation for n: n= 4a + 3 = 4 × 3b+ 3 = 12b + 3.
This expression was obtained from 24b + 6 through division by 2. It is important, that this transformation could not have occurred via the operation multiplying by 3 and adding 1 because 12b + 3 is 0 on module 3. Prior to this step, we would have had the number 48b + 12, and so forth. We observe that all of these numbers are multiples of 3. This observation leads us to hypothesize the existence of a cycle within this sequence. If such a cycle does not exist, then according to the principles of the Collatz conjecture, any number in this sequence must eventually converge to 1. This is because, in the absence of cycles, every number will ultimately engage with all possible integers through the iterative process defined by the conjecture.
Let’s consider the case, when b = 3c + 2. We know that c ≡ 2 (mod 3). It means that
n = 12b + 7 = 12 (3c + 2) + 7 = 36c + 31.
This expression was obtained from 72c + 62 through division by 2. 72c + 62 ≡ 2 (mod 3), so it was obtained from 144c + 124. It equals 1 modulo 3. So, it can be obtained from
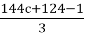
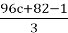
We are currently examining two remaining cases in our analysis. The first case to consider is when c ≡ 1 (mod 3). Given the expression for n:
4n = 12b + 7.
Substituting b with the expression derived from c: n= 12 (3c + 1) + 7 = 36c + 19. The value n = 36c + 19 is clearly odd, as it consists of an even term 36c and an odd term 19. Next, we compute: 3 × (36c + 19) + 1 = 108c+ 57 + 1 = 108c + 58. This expression, 108c + 58, is always even since both components, 108c (even) and 58 (even), yield an even result. We can simplify this expression by dividing by 2:
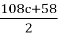
The term 54c + 29 is also always odd, as it consists of an even component 54c and an odd component 29. Now, we compute the following expression:
3 ×(54c + 29)+1 = 162c + 87 + 1 = 162c + 88.
This final expression, 162c + 88, is again even due to the fact that both terms are even.
And now let’s consider the case where c ≡ 0 (mod 3). We start with the expression for n:
n = 12b + 7.
Substituting b with 3c (since b can be expressed in terms of c):
n= 12 × 3c + 7 = 36c + 7.
It is evident that n is an odd number, as it can be expressed as the sum of an even number 36c and an odd number 7.
Next, we compute:
3 × (36c + 7) + 1 = 108c + 21 + 1 = 108c + 22.
The resulting expression, 108c + 22, is even since it can be represented as the sum of an even term 108c and another even term 22. To simplify this expression, we divide by 2:
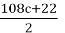
This expression, 54c + 11, remains odd, as it
consists of an even term 54 c and an odd term 11. Consequently, we apply the transformation for odd numbers:
3 × (54c + 11) + 1 = 162c + 33 + 1 = 162c + 34.
In summary, we have derived a sequence of transformations based on modular arithmetic and properties of odd and even numbers. Each step maintains the integrity of the mathematical operations while adhering to the specified conditions.
So, now it is time to draw some conclusions of our own research. We came to the point that proof of the Collatz conjecture for all natural numbers is equal to the proof of the Collatz conjecture for numbers of the type 162c + 34 and 162c + 88.
Analyzing articles
In this part of my work, I would like to analyze other authors’ researches. I want to start with 2 works of Gennadiy Usov. His first work suggests reasoning about the construction of a directed Collatz graph. The text identifies three primary stages in the construction of an oriented graph: construction of the main trunk of the oriented graph, development of the branches of the graph, determination of the sizes of the trunks and branches of the graph. The article represents an attempt to systematize the approach to the Collatz conjecture through a graphical representation of numerical sequences. [2]
His second article is about Absence of Cyclicity in Collatz Sequences. In particular, Gennadiy Usov uses Terrace’s proof to do it. [3]
Also, I decided to analyze the article of Kurmet Sultan. He claimed that he has a proof of the conjecture, but I found a mistake in his work. In particular, Kurmet Sultan asserts that if a number is odd and divisible by 3, the output of the function will be either 6m+1 or 6m−1, without providing any supporting evidence. An independent analysis reveals that a number of the form (6k + 3) × 3 + 1 = 18k + 10 is even, leading to
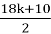
In David Barina’s work «Convergence verification of the Collatz problem», it was shown that all numbers till 2 in 68 degrees are checked. [4]
Of course, I couldn’t go through Terence Tao’s work on the Collatz Conjecture. Because work is very complicated and long, I would be brief: he demonstrated that almost all numbers, when iterated under the Collatz rules, eventually enter a small range of values (including 1). [5]
Also, I would like to highlight work that doesn’t direct connection with my one, but shows connection between collatz Conjecture, the Planck’s black body radiation density and Kurepa’s conjecture on left factorial function. It’s «Collatz hypothesis, together with its relation to Planck’s black body radiation, and Kurepa’s conjecture on left factorial function», written by Nicola Fabiano, Nikola Mirkov and Stojan Radenovic. [6]
Also, there are different varietes of code on python, which can calculate the Collatz sequence for some number. [7]
I attempted to prove this hypothesis under the assumption that the Collatz conjecture holds true for all integers up to a certain number n, and that n + 1 is the first integer for which this conjecture does not apply. In my exploration of various sources, I came across a study that discussed the concept of stopping time. This term is also referenced in other works [9–14], where it is analyzed in greater detail.
Conclusion
In this work was conducted own experience and analyze of some existed articles. In particular, more than a dozen relevant articles on this topic were studied and was proved correctness of hypotheses for all numbers except numbers of the form 162c + 34 and 162c + 88. Thus, the boundary of the correctness of the hypothesis was increased.
References:
- Winkler, Peter. Mathematical Puzzles: A Gourmet Collection. Moscow: MCNMO, 2024.
- Usov, Gennadiy. «The construction of a directed Collatz graph» Sci-Article.ru, 28 Oct. 2024, sci-article.ru/stat.php?i=1729763700.
- Usov, Gennadiy. «Finding Patterns When Presenting Evidence from Terrace (Collatz Conjecture).» Sci-Article.ru, 6 Nov. 2024, sci-article.ru/stat.php?i=1730784393.
- Barina, David. «Convergence Verification of the Collatz Problem.» The Journal of Supercomputing, vol. 77, no. 3, 1 July 2020, pp. 2681–2688, https://doi.org/10.1007/s11227–020–03368-x.
- Tao, Terence. «Almost All Orbits of the Collatz Map Attain Almost Bounded Values.» ArXiv:1909.03562 [Math], 6 June 2020, arxiv.org/abs/1909.03562.
- Fabiano, Nicola, et al. Collatz Hypothesis, Together with Its Relation to Planck’s Black Body Radiation, and Kurepa’s Conjecture on Left Factorial Function. 9 Oct. 2022.
- Pool, Team Python. «Understanding the Collatz Sequence in Python — Pythobyte.com.» Pythobyte.com, 27 Mar. 2021, pythobyte.com/collatz-sequence-python-45765/.
- Applegate, David, and Jeffrey C. Lagarias. Density Bounds for the 3x+1 Problem II. Krasikov Inequalities. 15 Dec. 1993. Accessed 10 Dec. 2024.
- J. Arsac (1986), Algorithmes pour verier la conjecture de Syracuse, C. R. Acad. Sci. Paris 303, Serie I, no. 4, 155–159. [Also: RAIRO, Inf. Theor. Appl. 21 (1987), 3–9. (MR87m:11128)
- C. Ashbacher (1992), Further Investigations of the Wondrous Numbers, J. Recreational Math. 24, 1–15.
- D. Boyd (1985), Which rationals are ratios of Pisot sequences?, Canad. Math. Bull. 343–349. (MR86j:11078).
- G.-G. Gao (1993), On consecutive numbers of the same height in the Collatz problem, Discrete Math., 112, 261–267. (MR94i:11018)
- L. E. Garner (1985), On heights in the Collatz 3n + 1 problem, Discrete Math. 55, 57–64. (MR86j:11005)
- T. Oliveira e Silva, Maximum excursion and stopping time record-holders for the 3x + 1 problem: Computational results, preprint 8











