Сравнение свойств двухмерного и трехмерного симплексов



В статье проводится сравнительный анализ свойств треугольника и тетраэдра.

Ключевые слова : геометрия, тетраэдр, треугольник, свойства.

В 10-м классе я познакомилась с новым разделом геометрии — стереометрией. Как правило, стереометрия и планиметрия изучаются независимо друг от друга. Общаясь со своими сверстниками, я обнаружила, что почти всем нам изучение стереометрии и решение задач дается с трудом, ввиду того, что курс геометрии значительно изменяется и требует от школьников творческих способностей и абстрактного мышления, представления, что некая плоскость не заканчивается, умения строить в воздухе параллельные, перпендикулярные плоскости и т. д. Но как только начинаешь чуть глубже погружаться в изучение стереометрии, понимаешь, сколько теорем, свойств построены на аналогии с планиметрией.

Актуальность работы состоит в том, что рассмотрение свойств треугольника и тетраэдра позволяет облегчить обучающимся понимание и усвоение курсов стереометрии.

Статья будет интересна многим ученикам, которые только начали изучать курс стереометрии после планиметрии, учителям математики, а также тем, кто заинтересован темой работы.

1. Некоторые свойства треугольника и тетраэдра

1. 1. Метод аналогии

Часто в точных науках, таких как физика и математика, большое внимание уделяется запоминанию алгоритмов решения задач, решению задач на вычисление, но не развивается тема логического мышления. Так, например, при решении различных задач школьники чаще всего пользуются именно алгоритмом, но возникают ситуации, когда одного алгоритма для решения недостаточно, поэтому приходится прибегать к сравнению и обобщению, методу аналогий.

Согласно словам автора в книге «Геометрия: метод аналогии»: «Аналогия — умозаключение, при котором один из некоторых сходных признаков двух предметов (явлений, процессов) и известного признака одного предмета делается умозаключение о том, что и другой предмет обладает этими сходными признаками». Говоря простыми словами, аналогия — это сходства предметов в каких-либо свойствах.

Аналогия важна тем, что она наводит нас на выдвижение гипотез, которые могут подтвердиться или не подтвердиться в результате выводов по аналогии, которые в свою очередь производятся на одном объекте, в то время как исследование проводится на другом объекте, что говорит о том, что метод аналогий даёт возможность получать новые знания.

1. 2. Треугольник и его пространственный аналог

Отметим три точки, не лежащие на одной прямой, и назовём их A, B, C . Если их соединить отрезками, то получится фигура, называемая треугольником (рис. 1).

Рис. 1. Треугольник

Если отметить точку S, не лежащую в плоскости ABC , и последовательно соединить ее с каждой из вершин треугольника, то мы получим фигуру (тело) под названием тетраэдр ( ABCS ). Она состоит из четырёх треугольников: ABS , BCS , ABC , ASC — они называются гранями тетраэдра. Их стороны являются рёбрами тетраэдра, вершины — вершинами тетраэдра (рис. 2).

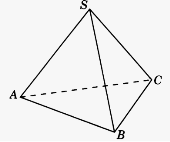
Рис. 2. Тетраэдр

1. 3. Медианы, высоты, биссектрисы

Медиана в треугольнике — отрезок, соединяющий вершину треугольника и серединой противоположной стороны. Все три медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины (доказательство см. [1], глава 7, параграф 3, пункт 64, задача 1).

Медиана в тетраэдре — отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани. Медианы тетраэдра пересекаются в одной точке и делятся точкой пересечения в отношении 3:1, считая от вершины (задача 8. 1 из [2]). Доказательство: достаточно доказать, что любые две медианы тетраэдра пересекаются и делятся точкой пересечения в отношении 3:1, считая от вершины (рис. 3). Пусть A ₁ и B ₁ — точки пересечения медиан граней BCD и ACD , O — середина ребра CD . Медианы AA ₁ и BB ₁ данного тетраэдра лежат в плоскости ABO , поэтому они пересекаются в некоторой точке M . Ясно также, что

.

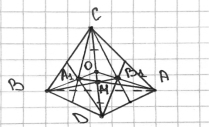
Рис. 3. Медианы в тетраэдре

Вывод: нет полного сходства между свойствами.

Высота в треугольнике — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В любом треугольнике высоты или их продолжения пересекаются в одной точке. Доказательство: проведём через каждую вершину треугольника ABC прямую, параллельную противоположной стороне. Получим треугольник A ₂ B ₂ C ₂ (рис. 4). Точки A , B , C являются серединами сторон этого треугольника. AB = A ₂ C и AB = CB ₂ как противоположные стороны параллелограммов ABA ₂ C и ABCB ₂ , поэтому A ₂ C = CB ₂ . Аналогично С ₂ A = АВ ₂ и С ₂ В = ВА ₂ . Кроме того, как следует из построения, СС ₁ перпендикулярно А ₂ В ₂ , АА ₁ перпендикулярно В ₂ С ₂ и ВВ ₁ перпендикулярно А ₂ С ₂ . Таким образом, прямые АА ₁ , ВВ ₁ и СС ₁ являются серединными перпендикулярами к сторонам треугольника А ₂ В ₂ С ₂ . Следовательно, они пересекаются в одной точке (доказательство — [1], глава 8, параграф 3, пункт 76).

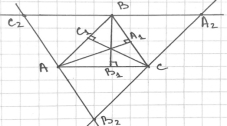
Рис. 4. Высоты в треугольнике

Высота в тетраэдре — отрезок, соединяющий вершину с точкой плоскости противоположной грани и перпендикулярен этой плоскости. Пересекаются ли они в одной точке? (Задача 8. 5 [2]). Рассмотрим треугольник ABC , в котором угол A не прямой, и восставим к плоскости треугольника перпендикуляр AD . В тетраэдре ABCD высоты, проведённые из вершин C и D , не пересекаются (рис. 5).

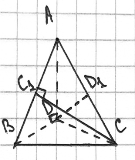
Рис. 5. Высоты в тетраэдре

Вывод: нет сходства между свойствами.

Биссектриса в треугольнике — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Биссектрисы треугольника пересекаются в одной точке, которая равноудалена от сторон треугольника. Точка является замечательной, является центром вписанной окружности, поэтому и равноудалена от сторон треугольника.

Биссектриса в тетраэдре — отрезок, соединяющий вершину тетраэдра с некоторой точкой противолежащей грани. Биссектрисы тетраэдра пересекаются в одной точке, каждая точка биссектрисы равноудалена от трёх плоскостей граней тетраэдра. (Задачи 2. 30, 2. 33 [2]). Доказательство: биссекторные полуплоскости двугранных углов тетраэдра при рёбрах DA , DB и DC пересекаются по лучу DD ₁ , где D ₁ – некоторая точка грани АВС . Биссекторная полуплоскость двугранного угла тетраэдра при ребре АВ пересекает отрезок DD ₁ в точке S , равноудалённой от плоскостей граней тетраэдра. Биссекторные полуплоскости двугранных углов тетраэдра при рёбрах ВС и СА пересекают этот отрезок в той же самой точке S . Эта точка — точка пересечения биссекторных полуплоскостей двугранных углов тетраэдра. Биссекторные полуплоскости трёх двугранных углов тетраэдра пересекаются по лучу с началом в вершине тетраэдра. Согласно уже доказанному в предыдущих задачах учебника этот луч — множество точек, расположенных внутри этих двугранных углов и равноудалённых от плоскостей их граней (рис. 6).

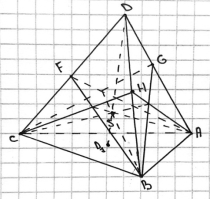
Рис. 6. Биссектриса в тетраэдре

Вывод: есть полное сходство между свойствами.

1.4. Теоремы Пифагора, косинусов, Менелаяна плоскости и их версии для тетраэдра

Теорема Пифагора — одна из самых важных теорем в геометрии, которая связана с прямоугольным треугольником. Она широко используется при решении задач планиметрии любой сложности и гласит о том, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов ([1],глава 6, параграф 3, пункт 55). Доказательство: достроим данный нам прямоугольный треугольник до квадрата со стороной . Площадь этого квадрата равна . С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна , и квадрата со стороной , поэтому

.

Таким образом, , откуда (рис. 7).

Рис. 7. Теорема Пифагора для треугольника

Тетраэдр, у которого три угла при одной вершине прямые, называется прямоугольным. Теорема Пифагора для тетраэдра: в прямоугольном тетраэдре квадрат площади грани-гипотенузы равен сумме квадратов площадей граней-катетов. Докажем теорему (рис. 8). Доказательство: пусть нам дан прямоугольный тетраэдр ABDC , такой что DB BC , DB BA , AC AB и BC=a , AB= b,DB=c .

, , .

Проведём DG — апофему тетраэдра, необходимую для вычисления площади грани ADC . Рассмотрим треугольник ADG :

По теореме Пифагора:

.

Рассмотрим треугольник DBA : ; .

Рассмотрим треугольник DBC : ; .

Рассмотрим треугольник ACB :

; .

.

Пусть AG=x , тогда , .

Рассмотрим треугольник DHB : по теореме Пифагора:

= .

Отсюда .

.

Итак, .

.

.

Что и требовалось доказать.

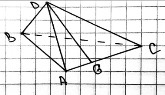
Рис. 8. Теорема Пифагора для тетраэдра

Теорема косинусов для треугольника была давно доказана с помощью теоремы Пифагора. Звучит она так: квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения их на косинус угла между ними.

Рассмотрим и докажем пространственный аналог теоремы косинусов: квадрат площади любой грани тетраэдра равен сумме квадратов площадей трёх остальных граней без удвоенных произведений площадей этих граней, взятых попарно, и косинусов двугранных углов между ними. Доказательство: рассмотрим тетраэдр ABCD (рис. 9):

, , ,

, аналогично угол .

Рассмотрим треугольник BPC :По теореме косинусов:

.

Умножим это равенство на :

Получаем:

(1)

Рассмотрим треугольник AMD . По теореме косинусов:

.

Умножим это равенство на :

.

Получаем:

. (2)

В равенстве (1) и (2) одинаковые левые части, поэтому можно приравнять и правые:

= . (3)

Аналогично для рёбер AC и DB , AB и DC :

= . (4)

= . (5)

Сложим полученные равенства (3), (4), (5):

- + .

Получаем:

. (6)

Сумма площадей ортогональных проекций боковых граней на основание равно площади основания:

. (7)

Подставим (7) в (6):

То есть

Следствие:

Что и требовалось доказать.

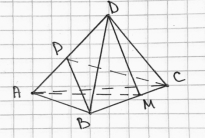
Рис. 9. Теорема косинусов для тетраэдра

Рассмотрим теорему Менелая на конкретном примере:

Если на сторонах PQ и QC треугольника PQC взяты соответственно точки C ₁ , P ₁ , а точка Q ₁ взята на продолжении стороны PC за точку C , то точки C ₁ , P ₁ , Q ₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство

(8)

Доказательство:

1. Докажем необходимость (если точки C ₁ , P ₁ , Q ₁ лежат на одной прямой, то выполнено равенство (8)).

Проведём CM так, что CM параллельно PQ (рис. 10). Треугольник PC ₁ Q ₁ подобен треугольнику CMQ ₁ , поэтому

. (9)

Треугольник C ₁ QP ₁ подобен треугольнику P ₁ MC , поэтому

. (10)

Перемножим равенства (9) и (10):

,

.

Отсюда получаем:

.

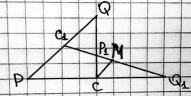
Рис. 10. Теорема Менелая (необходимость)

2. Докажем достаточность (если выполняется равенство (8), то точки C ₁ , P ₁ , Q ₁ лежат на одной прямой)

Воспользуемся методом «от противного».

Предположим, что C ₁ , P ₁ , Q ₂ лежат на одной прямой, а точка Q ₁ не лежит на этой прямой (рис. 11), тогда:

(11)

и

.

Разделим (4) на (1) и получим:

=1.

Из этого следует, что , поэтому что Q ₁ совпадает с Q _2.

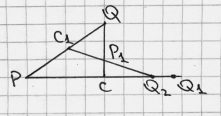
Рис. 11. Теорема Менелая (достаточность)

Что и требовалось доказать.

Рассмотрим, как работает теорема Менелая в конкретном тетраэдре:

В произвольном тетраэдре PKLM точки Q , S , Y , X принадлежат рёбрам KP , PL , LM , KM соответственно (рис. 12). Для того, чтобы точки Q , S , Y , X принадлежали одной плоскости необходимо и достаточно, чтобы выполнялось следующее равенство:

(12)

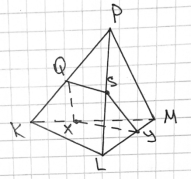
Рис. 12. Теорема Менелая для тетраэдра

Доказательство:

1. Докажем необходимость.

Пусть четырёхугольник XQSP — сечение γ тетраэдра KLMP . Проведём перпендикуляры к плоскости из вершин тетраэдра:

Рассмотрим развёртку и подобные треугольники и получим (рис. 13):

.

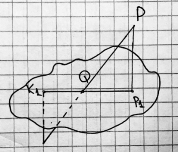
Рис. 13. Теорема Менелая для тетраэдра (необходимость)

Аналогично с остальными подобными треугольниками:

, , .

Перемножив все получившиеся равенства получим:

.

Сокращаем:

.

2. Докажем достаточность:

Предположим, что равенство (12) выполняется, но точки Q , S , Y , X не лежат в одной плоскости:

Проведем через X , Y , S плоскость λ, которая пересечёт PK в некоторой точке Q ₁ , отличной от Q , поэтому , поэтому равенство (1) выполняться не будет. Поскольку мы пришли к противоречию с исходным условием, то наше предположение неверно и плоскость λ пройдёт через точку Q .

2. Решение задач

Задача 1 ([3], задача 14 варианта 206) . Точки M, N, K принадлежат рёбрам AD, AB, BC тетраэдра ABCD , причем AM:MD = 2:3, BN:AN = 1:2, BK=KC (рис. 14).

а) Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, K .

б) Найдите отношение, в котором секущая плоскость делит ребро CD .

Решение: а)

1. .

2. Так как

3. — искомое сечение тетраэдра.

б) AM:MD = 2:3, BN:AN = 1:2, BK=KC=x по условию. Из пространственной теоремы Менелая следует:

.

.

.

.

Ответ: DP:PC=3:1 .

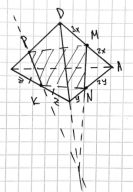
Рис. 14. Теорема Менелая в тетраэдре

Задача 2 (значения взяты из задачи 66 [4]) . В тетраэдре DABC дано: ADB = 54° , BDC= 72° , CDA = 90 °, DA = 20 см , BD = 18 см , CD = 21 см . Найдите площадь грани-гипотенузы (рис. 15).

Решение:

По пространственной теореме Пифагора:

.

.

Ответ: 312 см ² .

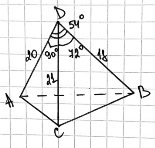
Рис. 15. Теорема Пифагора в тетраэдре

Заключение

После проделанной работы можно сделать вывод, что были достигнуты поставленные цели, а именно, изучены и сравнены некоторые из свойств треугольника и тетраэдра, которые наиболее ярко показывают их сходства, показано их применение в некоторых задачах. Для этого было изучено большое количество литературы, пособий и задачников.

В результате исследования получены результаты о том, что теорема Менелая, теорема Пифагора, теорема косинусов и некоторые замечательные линии треугольника имеют свои аналогии в стереометрии. Эта работа полезна, так как во все времена в математике ценились рациональные и наиболее быстрые способы решения задач, применение которых упрощает процесс решения и делает его менее громоздким.

Литература:

1. Геометрия. 7–9 классы: учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. — М. : Просвещение, 2010. — 384 с. :ил. — ISBN 978–5-09–023915–8.
2. Прасолов В. В. Задачи по стереометрии: Учебное пособие. — М. : МЦНМО, 2010. — 352 с. : ил. 978–5-94057–605–1
3. Сайт по подготовке к ЕГЭ по математике Ларина Александра Александровича https://alexlarin. net/
4. Геометрия 10–11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. ]. — 22-е изд. — М. :Просвещение, 2013. — 255 с. : ил. — (МГУ — школе). — ISBN 978–5-09–030854–0.