Исследование модели сейсмоизолирующей системы Курзанова — Семенова



Приведены результаты исследования модели (макета) сейсмоизолирующей системы Курзанова — Семенова. Проведены измерения силы, необходимой для удержания системы в равновесии (удерживающей или уравновешивающей силы), при отклонении сейсмоизолированной части (суперструктуры) в горизонтальном направлении. Построены графики зависимости удерживающей силы от величины отклонения. Показано, что с ростом отклонения модуль удерживающей силы уменьшается. Дальнейшее уменьшение отклонения демонстрирует гистерезисный характер поведения указанной зависимости.

Ключевые слова: землетрясение, сейсмостойкое строительство, трубобетонная опора, сейсмоизолирующие опоры, сейсмограмма, акселерограмма, уравнение движения.

Введение

Большое число густонаселенных городов в сейсмически активных регионах мира (Япония, Турция, Кавказ и др.) является самым весомым аргументом развития исследований в области сейсмостойкого строительства. Одним из видов сейсмоизолирующих систем являются кинематические системы (Черепинского, Курзанова — Семенова и др.) [1–3]. Среди разного вида таких систем выгодно выделяется система Курзанова — Семенова, опоры которой имеют трубобетонную структуру [4]. Основное преимущество сейсмоизолирующих опор Курзанова — Семенова в простоте и, соответственно, высокой технологичности. В силу этого они могут изготавливаться не только в заводских условиях, но и непосредственно на строительной площадке. Еще одно немаловажное достоинство в том, что такая система имеет пороговое значение ускорения основания, при котором она «включается» в работу. Благодаря этому система малочувствительна к низкоинтенсивным воздействиям (сейсмическим или ветровым).

В данной статье приведены результаты экспериментального исследования модели (рис. 1) сейсмоизолирующей системы Курзанова — Семенова. Проведены соответствующие расчеты и сравнения с ранее известными данными, сделаны выводы и намечены направления дальнейших исследований с использованием модели.

Рис. 1. Модель сейсмоизолирующей системы Курзанова — Семенова: 1 — основание, фундамент, земля; 2 — опора; 3 — сейсмоизолированная, надземная часть (суперструктура)

Основная часть

При выведении системы из положения равновесия (отклонении в горизонтальном направлении) возникают возвращающие силы, которые пытаются вернуть систему в исходное (основное) состояние, когда опоры находятся в строго вертикальном положении (рис. 2). Эту возвращающую силу можно уравновесить равной по модулю и противоположной по направлению удерживающей (уравновешивающей) силой

(рис. 2).

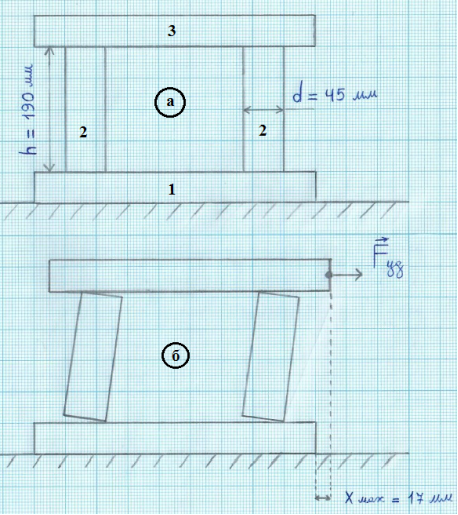
Рис. 2. Схематическое изображение модели системы Курзанова — Семенова, в состоянии равновесия (а) и выведенной из него (б) (1 — основание, фундамент, земля; 2 — опора; 3 –суперструктура)

Были проведены эксперименты по измерению удерживающей силы при различных массах сейсмоизолированной части. Измерения силы проводились с помощью учебного пружинного динамометра. Грузами, использовавшимися для увеличения массы суперструктуры, служили книги (учебники по физике). Все массы определялись с помощью того же учебного динамометра. Для определения линейных размеров использовалась обычная линейка и штангенциркуль. Фотографии экспериментальной установки, без дополнительной массы и при нагружении таковой, приведены на рисунках 3 и 4, соответственно.

Рис. 3. Фото экспериментальной установки (ненагруженная изолированная часть)

Рис. 4. Фото экспериментальной установки (нагруженная изолированная часть)

Динамика процесса измерений была следующей. К находящейся в основном состоянии системе начинает прикладываться отклоняющая (удерживающая) сила (рис. 2–4), сила упругости от растянутой пружины динамометра (рис. 3, 4). Динамометр показывал и значение этой силы. Увеличение силы производилось удалением штатива с прикрепленным к нему динамометром от макета, а уменьшение силы — приближением штатива к нему (рис. 3, 4).

Постепенное увеличение силы приводило к тому, что при некотором ее значении F ₁ система резко отклонялась от положения равновесия (х=0) до максимально возможного для данной модели отклонения (х=х _max =17 см). В процессе отклонения значение удерживающей силы постепенно уменьшалось и при х = х _max =17 см становилось равным F ₂ ( F ₂ < F ₁ ). К сожалению, возможности данной экспериментальной установки не позволяют измерять значения удерживающей силы для значений координаты x , лежащих в пределах от х =0 до х = х _max . Невозможно также измерить и сами промежуточные координаты х , т. к. движение от х =0 к х = х _max , и обратно, происходит скачкообразно.

Дальнейшее постепенное «отпускание» (уменьшение отклоняющей силы) показывало, что уменьшение силы от значения F ₂ до некоторого значения F ₃ ( F ₃ < F ₂ ) не приводило к уменьшению координаты x , она оставалась равной х = х _max . При значении силы, равном F ₃ , происходило резкое отпускание системы и координата уменьшалась до х =0. При стремлении координаты х к нулю (системы к основному состоянию) величина удерживающей силы увеличивалась от значения F ₃ до F ₄ . Причем F ₃ < F ₄ < F ₁ . Выше уже отмечалось, что установка не позволяет отследить значения удерживающей силы в пределах 0< х < х _max .

Динамика описанных процессов отражена на графике, представленного на рисунке 5. Измеренные значения удерживающей силы при различных положениях и массах изолированной части внесем в таблицу 1.

Таблица 1

Сводные результаты измерений

№	Масса сейсмоизолированной части M , кг	х =0		х = х max
		F 1 , Н	F 2 , Н	F 3 , Н	F 4 , Н
1	1.64	2.8	2.3	1.5	2.3
2	2.62	3.8	3.2	2.0	2.6
3	4.14	5.5	5.0	3.2	3.8
4	5.58	7.0	6.0	4.2	5.0

По числовым данным из таблицы 1 (для серий измерений № 1 и № 4) построим график зависимости удерживающей силы от координаты х (рис. 5).

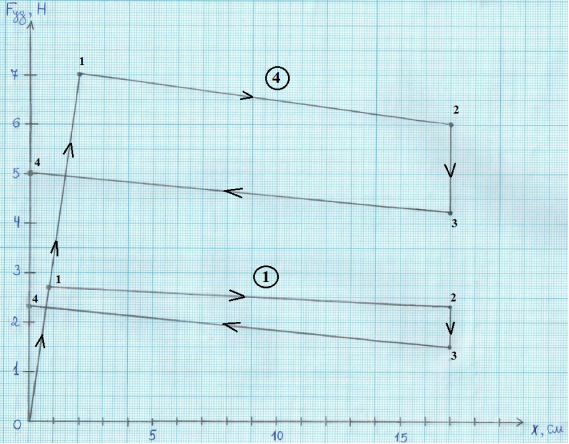
Рис. 5. Зависимость удерживающей силы от величины отклонения (координаты). Стрелками указано направление развития процесса нагрузки-разгрузки. Цифры около точек соответствуют состояниям, указанным в таб. 1 для серий измерений 1 и 4 (указано цифрами в кружочках)

Из таблицы 1 и графика (рис. 5) можно видеть, что увеличение массы сейсмоизолированной части приводит к увеличению удерживающей силы. Это, конечно, очевидно, т. к. увеличение массы приводит к увеличению силы тяжести, а она и является основной причиной стремления системы к первоначальному устойчивому положению. Прямой пропорциональности между силой и массой, однако, не наблюдается.

Также можно отметить, что график зависимости имеет «петлеобразный» (гистерезисный) характер. Переход из состояния 2 в 3, когда система остается в максимальном отклонении от положения равновесия, происходит без изменения координаты. Объяснить это можно «помощью» силы трения трения. Предположим, что ее предельное значение (при котором покой переходит в скольжение) равно разнице между F ₂ и F ₃ :

. (1)

Известно, что предельное значение силы трения пропорционально весу тела. Из таблицы 1 можно видеть, что с увеличением массы M растет и разница между значениями силы F ₂ и F ₃ . Так при увеличении массы в раза разница возросла в раза. А при увеличении массы в раза разница возросла в раза. Полученный результат подтверждает пропорциональность и свидетельствует в пользу предположения, что «гистерезисность» зависимости можно объяснить влиянием силы трения.

В работах научно-исследовательской группы Семенова С. Ю., например, в [5], также отмечается гистерезисность зависимости удерживающей силы от величины смещения суперструктуры из положения равновесия.

В работе [6] получено теоретическое выражение для расчета удерживающей силы:

, (2)

где — количество опор, — масса сейсмоизолированной части, — масса одной опоры, — ускорение свободного падения, — диаметр опорной части опоры (рабочей пластины), — высота опоры,

–горизонтальное смещение, — вертикальное смещение.

Формула (2) действительно подтверждает убывающий вид зависимости от (см., например, рис. 6 в [6]). Однако, при выводе формулы (2) не учитывалось влияние силы трения, т. е. работа опоры при ее отклонении считалась в режиме «идеального шарнира». Поэтому гистерезисность зависимости формулой (2) не отражается.

Проведем с помощью данной формулы расчет для одного из случаев нагружения (см. табл. 1). Измеренные значения массы, диаметра и высоты: кг, мм, мм. Число опор . Максимальное отклонение х _max =17 см. Ввиду малости смещения по вертикали в сравнении с будем полагать

Тогда для случая 1 (см. таблицу 1):

1. при Н.
2. при мм Н.

Тогда для случая 4 (см. таблицу 1):

1. при Н.
2. при мм Н.

Для визуализации и сравнения построим экспериментальную и рассчитанную по формуле (2) зависимости удерживающей силы от координаты х на одном графике (рис. 6). Построение проведено для серии измерений (случая) 4 (см. табл. 1 и расчеты выше).

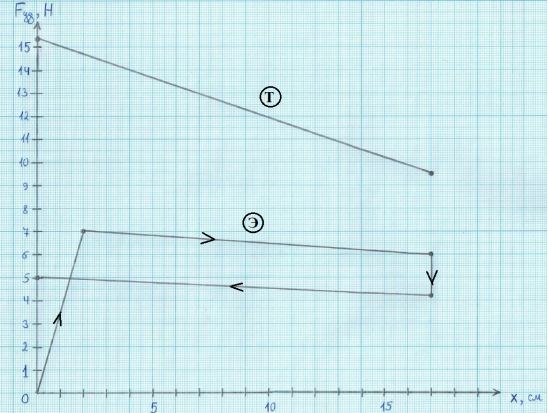
Рис. 6. Зависимость удерживающей силы от величины отклонения: эксперимент и теория. Буквы в кружочках означают теорию (Т) и эксперимент (Э), соответственно

Проведенные расчеты и график, представленный на рис. 6, показывают, что теоретически рассчитанные значения удерживающей силы превышают определенные ее значения при экспериментальном исследовании. Основная причина, как уже отмечалось выше, кроется в неучете математико-физической моделью [6] силы трения, т. е. связи между элементами системы подразумевались идеальными. Кроме того, по этим же причинам, модель не предсказывает гистерезисный характер зависимости, поэтому и теоретическая зависимость, представленная на рис. 6 и описываемая формулой (2), не устанавливает различия между процессами нагрузки системы (увеличение отклонения) и ее разгрузки (уменьшение отклонения).

Следует отметить, что значения диаметра опорной части и высоты опоры определены весьма приблизительно. Это связано с конструкцией опор данного макета (модели) — она является неразборной. Семенов С. Ю. любезно предоставивший авторам данный макет для исследования, к сожалению, геометрические его характеристики забыл. Эта приближенность, конечно, вносит некоторые неточности в расчеты, проводимые по формуле (2). Однако эти погрешности имеют небольшую относительную величину и не влияют на характер обобщающих рассуждений.

Авторы надеются продолжить начатую работу. Следующим шагом могут быть исследования по поведению макета (модели) при имитации сейсмического воздействия на нее.

Заключение

Эксперименты с моделью (макетом) сейсмоизолирующей системы Курзанова — Семенова и проведенные соответствующие им расчеты, сопоставление полученных результатов с известными ранее данными показали, что:

1. подтвержден гистерезисный характер поведения удерживающей (уравновешивающей) силы от величины отклонения суперструктуры от положения равновесия;
2. предположение о влиянии силы трения на гистерезисность зависимости удерживающей силы от величины отклонения подтверждается соответствующим оценочным расчетом;
3. расчетные значения удерживающей силы превышают определенные при прямом эксперименте, подтверждая необходимость введения в математическую модель силы трения;
4. экспериментальные исследования с использованием малогабаритного (мелкомасштабного) макета перспективны и позволяют делать выводы достаточно высокой научной степени.

Авторы статьи благодарят Семенова Станислава Юрьевича за макет сейсмоизолирующей системы, который он передал им для исследований.

Литература:

1. Тяпин А. Г. Плоские колебания жесткого сооружения на кинематических опорах: общий случай геометрии // Сейсмостойкое строительство. Безопасность сооружений. — 2020. — № 4. — С. 41–54. — DOI 10.37153/2618–9283–2020–4–41–54. — EDN KZFLQK.
2. Тяпин А. Г. Уравнение плоских колебаний жесткого сооружения на кинематических опорах А. М. Курзанова // Сейсмостойкое строительство. Безопасность сооружений. — 2020. — № 5. — С. 19–31. — DOI 10.37153/2618–9283–2020–5–19–31. — EDN DICCJY.
3. Тяпин А. Г. Плоские колебания жесткого сооружения на кинематических опорах А. М. Курзанова // Сейсмостойкое строительство. Безопасность сооружений. — 2020. — № 6. — С. 27–38. — DOI 10.37153/2618–9283–2020–6–27–38. — EDN NQIZTD
4. Курзанов А. М., Семёнов С. Ю. Трубобетонная сейсмоизолирующая опора. Патент на изобретение RU 2477353 C1, 10.03.2013. Заявка № 2011126415/03 от 27.06.2011.
5. Сухарев, Ф. И. Реакция здания с кинематической системой сейсмоизоляции на ветровое воздействие и её анализ средствами Лира-САПР / Ф. И. Сухарев, Н. А. Иваненко, С. Ю. Семенов // Инженерный вестник Дона. — 2021. — № 1(73). — С. 271–284. — EDN COZMKP.
6. Сейсмоизолирующие опоры Курзанова — Семенова: теория и эксперимент / А. М. Кириллов, Ф. И. Сухарев, Н. А. Иваненко, С. Ю. Семенов // Вестник евразийской науки. — 2024. — Т. 16, № 4. — EDN IOHUNT.