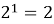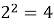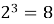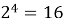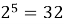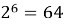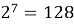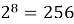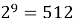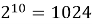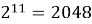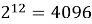Закономерности изменения последних цифр степеней с натуральными показателями (опыт решения олимпиадных задач)



Олимпиадные задачи по математике являются очень сложными и требуют глубокого понимания математических концепций и владения определенными средствами решения. Одними из таких являются задачи на степени с натуральными показателями. В статье продемонстрировано, как выявленные закономерности в последних цифрах степеней позволяют получить более оригинальное и быстрое решение олимпиадных задач по математике.

Ключевые слова: олимпиадная задача, степень с натуральным показателем, закономерности последних цифр степеней.

Окружающая действительность зачастую требует от человека принимать нестандартные решения. Успех в этом деле, в первую очередь, зависит от умений анализировать и оценивать суждения окружающих, конструировать собственное видение и аргументы, выстраивать свою позицию. Наличие этих умений позволит охарактеризовать его как критически мыслящую личность [1].

Навыки мышления необходимы каждому человеку — каким бы делом не занялся в своей жизни, начиная от решения бытовых или профессиональных задач, заканчивая творческой деятельностью. Так, согласно данным Всемирного экономического форума, навык критически мыслить входит в ТОП-5 компетенций, необходимых для успешного и эффективного функционирования в 2022 году и в десятку самых важных и востребованных навыков к 2025 году [2]. Математика является одним из мощным инструментом формирования такого мышления.

Традиционно математические задачи делятся на рутинные и творческие. Рутинные задачи обладают заранее известным набором действий. Чтобы их решить, нужно определить тип задачи и действовать по заданному алгоритму. С другой стороны — творческие задачи, предлагающиеся на различных состязаниях, в первую очередь, на олимпиадах. Олимпиадные задачи по математике являются сложными и требуют глубокого понимания математических концепций и владения определенными средствами решения [4].

На уроках математики мы изучили степени с натуральным показателем и их свойства. В целом, все задачи мне были понятны, просты в решении. Отметив это, мой научный руководитель предложил мне, с первого взгляда, очень трудную задачу. Необходимо было найти последнюю цифру суммы Тогда я подумал, что должен быть какой-нибудь рациональный подход к решению. Мне стало интересно, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа? В данной статье рассмотрено, как использование данных закономерностей позволяет привести более быстрое и оригинальное решение олимпиадных задач по математике.

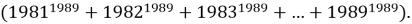
Определение 1. Степень числа с натуральным показателем называется произведение

множителей, каждый из которых равен т. е. выражение вида [3].

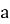
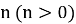
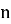
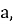
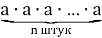
Пример 1.

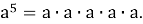
Проведем небольшое исследование: выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа , где — натуральное число, с изменением показателя . Оформим результаты в таблице (табл. 1).

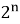
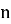
Таблица 1

Степени числа 2

Вывод : в результате заполнения таблицы степеней 2, нетрудно заметить, что последние цифры степени повторяются через каждые четыре шага. В перспективе это позволит выяснить последнюю цифру любой степени числа 2. Например, степень 4 столбца).

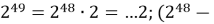
Справедливо поставить следующий вопрос: «Существует ли закономерность для других чисел?». С этой целью нами была составлена таблица для чисел от до . Ее фрагмент представлен ниже (табл. 2).

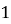
Таблица 2

Степени натуральных чисел (от 1 до 10)

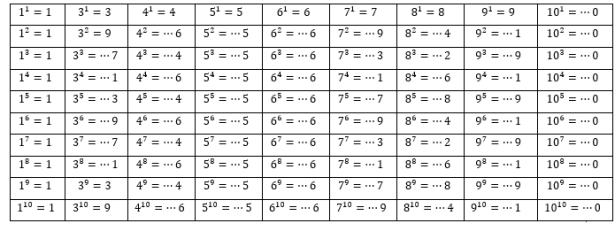
Исходя из полученных результатов, справедливо отметить следующие закономерности:

– во-первых, натуральные степени чисел 1; 5; 6 и 10 оканчиваются самим числом;

– во-вторых, степени чисел 4 и 9 оканчиваются цифрами, повторяющимися через каждый шаг;

– в-третьих, степени чисел 3; 7 и 8 оканчиваются цифрами, повторяющимися через каждые 4 шага.

В этой связи актуален вопрос: «Каким образом выяснить последнюю цифру степени с учетом периодичности вариантов?». Рассмотрим следующую задачу: «На какую цифру оканчивается степень »

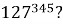
Во-первых, следует отметить, что для любого натурального основания, важно отмечать последнюю его цифру. Например, у числа « » — число « ».

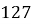
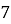
Во-вторых, использовать таблицу 2 — в нашем случае, столбец со степенями числа « ». Так как, период последних цифр степени числа « » равен , то и у степени числа «

» он будет аналогичным.

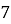
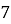
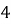
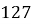
В-третьих, необходимо определить остаток от деления показателя степени на период. В нашем случае, (ост. ). Это означает, что последняя цифра степени (или, исходя из второго пункта — степени ) совпадет с последней цифрой степени , т. е. .

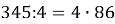
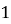
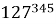
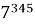
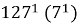
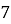
На основании рассмотренного примера, можно предложить следующий задачный материал.

Задача 1. На какую цифру оканчивается выражение

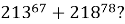
Решение . Рассуждая аналогичным образом, установим, что последняя цифра степени совпадет с соответствующей цифрой степени Учитывая периодичность последних цифр степени числа « » (табл. 2), то оканчивается на цифру « ». Схожим образом получаем, что оканчивается цифрой «4». Складывая получившиеся результаты, выясняем, что последней цифрой выражения будет .

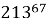
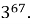
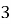
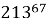
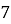
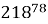
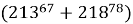
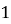
Задача 2. Докажите, что делится без остатка на 10.

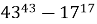
Решение. Выясним последние цифры степеней и Опираясь на таблицу 2, с учетом периодичности последних цифр для степеней чисел «3» и «7», установим, что и Очевидно, что разность степеней будет оканчиваться «0». А согласно признаку делимости, это означает, что кратно 10.

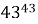
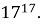
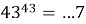
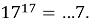
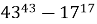
Задача 3. Докажите, что число является составным.

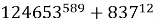
Решение. Начнем с определения понятия «составное число». Итак, составное число — это натуральное число, имеющее делители, отличные от единицы и самого себя (нетривиальные делители). Поэтому, в качестве одной из стратегии решения задачи, определим последнюю цифру данной суммы. Так, если она окажется четной, то исходное число будет составным.

Получили, что и

Значит, будет оканчиваться нулем, что означает наличие нетривиального делителя 2. Тогда, согласно определению, является составным.

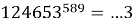
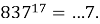
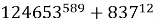
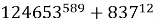
Задача 4. Докажите, что число не делится нацело на 15.

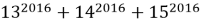
Решение. Решим задачу от противного. Пусть данное выражение кратно 15, а значит делится на и на оба условия должны выполнятся. Итак, степень оканчивается цифрой «1», оканчивается цифрой «

», оканчивается цифрой «5». Значит, последней цифрой числа ( ) будет «2». Число кратно 5 тогда, когда оно оканчивается цифрой « » или « », поэтому данное число не делится на , а значит и на .

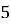
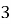
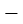
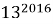
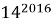
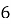
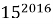
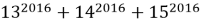
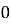
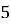
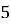
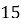
Задание 5. Найдите последнюю цифру суммы

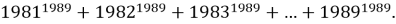
Решение. Вычисляя последние цифры степеней, получим:

Получаем: Следовательно, ( ) оканчивается на 5.

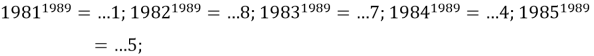
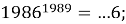
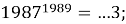
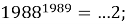
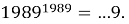
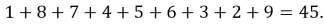
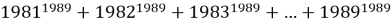
Таким образом, теория степени с натуральным показателем и ее приложения являются эффективными ресурсами решения олимпиадных задач по математике. Изученные закономерности изменения последних цифр степени натурального числа станут мощной отправной точкой для развития теории и решения более сложных задач олимпиадной тематики.

Литература:

1. Вередюк О. В., Черных Е. А. Олимпиадники поколения Z: поведенческие установки на рынке труда // Уровень жизни населения регионов России. — 2022. — Том 18. — № 1. — С. 79–91.
2. Привалова Г. Ф., Ткаченко Л. А., Ткаченко А. В. Предметные олимпиады как способ повышения качества образования студентов вуза культуры // Профессиональное образование в России и за рубежом. — 2020. — № 2(38). — С. 160–165.
3. Смолин Ю. Н. Алгебра и теория чисел: учеб. пособие для студ. Физ.-мат. фак. высших пед. учеб. заведений / Ю. Н. Смолин. — 3-е изд., испр. — М.: Флинта: Наука, 2006. — 463 с.
4. Усмонов Х. З., Останов К., Махмудов Х. Ш. Об использовании различных нестандартных упражнений в развитии творческой активности учащихся на уроках математики // Наука и образование сегодня. — 2021. — № 9(68). — С. 5–6.